- Parametarske i neparametarske tehnike - I deo
- Parametarske i neparametarske tehnike - II deo
- Definisanje pretpostavki - I deo
- Definisanje pretpostavki - II deo
- Definisanje pretpostavki - III deo
- Greška prve vrste, greška druge vrste i moć testa - I deo
- Greška prve vrste, greška druge vrste i moć testa - II deo
- Planirana poređenja / naknadne analize - I deo
- Planirana poređenja / naknadne analize - II deo
- Veličina uticaja - I deo
- Veličina uticaja - II deo
- Nedostajući podaci
- Parametarske vs. neparametarske tehnike
Za ispitivanje značajnih razlika između grupa postoji ceo niz tehnika. Te tehnike su vrlo složene i oslanjaju se na obimnu teoriju i statistička načela. Naime, programski paket SPSS sadrži mnogo statističkih tehnika, a u ovoj i u narednim lekcijama će se obraditi samo one glavne, i to i parametarske i neparametarske. Parametarske tehnike počivaju na više pretpostavki o populaciji iz koje je izvučen uzorak (npr. da su rezultati normalno raspodeljeni) i prirodi tih podataka (da su mereni na intervalnim skalama). Neparametarske tehnike nemaju tako stroge pretpostavke i često su prikladnije za male uzorke ili kada su prikupljeni podaci izmereni samo na ordinalnim skalama (čiji se iznosi mogu rangirati). U narednoj tabeli dat je spisak svih tehnika koje će biti obrađene kako u ovoj, tako i u narednim lekcijama.
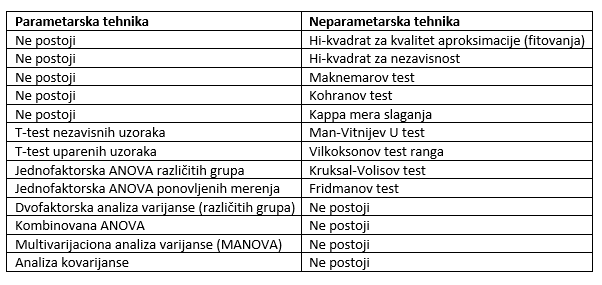
Slika-1 Lista parametarskih tehnika i njihovih neparametarskih ekvivalenata obrađenih u ovoj i u narednim lekcijama
U lekciji 6. je bio definisan proces odlučivanja o tome koja je statistička tehnika prikladna za konkretno istraživačko pitanje. Odgovor se menja u zavisnosti od prirode istraživačkog pitanja, vrste podataka na raspolaganju i broja promenljivih i grupa. Evo ključnih tačaka koje treba imati u vidu kada se traži prikladna statistička tehnika:
- t-testovi se upotrebljavaju kada imate samo dve grupe (npr. muškarci/žene) ili dve tačke u vremenu (npr. pre intervencije, posle intervencije);
- tehnike analize varijanse se upotrebljavaju kada imate dve ili više grupa ili tačaka u vremenu;
- tehnike uparenih uzoraka ili ponovljenih merenja upotrebljavaju se za testiranje istih ljudi u više navrata, ili kada imate uparene uzorke;
- tehnike analize različitih grupa i nezavisnih uzoraka upotrebljavaju se kada su subjekti u svim grupama različiti ljudi (ili nezavisni);
- jednofaktorska analiza varijanse se upotrebljava kada imate samo jednu nezavisnu promenljivu (npr. pol);
- dvofaktorska analiza varijanse se upotrebljava kada imate dve nezavisne promenljive (pol, starosna grupa);
- analiza varijanse više zavisnih promenljivih (multivarijaciona analiza) upotrebljava se kaada imate više zavisnih promenljivih (anksioznost, depresija) i
- analiza kovarijanse (ANCOVA) upotrebljava se kada treba statistički kontrolisati (ukloniti) uticaj dodatne, remetilačke promenljive koja utiče na vezu između nezavisne i zavisne promenljive.
Pre nego što se upustimo u istraživanje nekih dostupnih tehnika, treba razmotriti više zajedničkih pitanja. Te teme će biti relevantne za mnoge naredne lekcije, pa ćete se vraćati ovde kako budete prolazili kroz ostatak nastavnog materijala iz ovog predmeta.
Na nekim opštim pretpostavkama počivaju sve ovde razmotrene parametarske tehnike (npr. t-testovi, analiza varijanse), a pojedine tehnike se zasnivaju i na dodatnim pretpostavkama. Opšte pretpostavke će biti predstavljene u ovom poglavlju, a specifične pretpostavke u narednim poglavljima, (lekcijama), po potrebi. Trebalo bi da se vraćate na ovaj uvod kada budete primenjivali neku od tehnika predstavljenih u narednim lekcijama. Razmatranje postupka provere zadovoljavanja pretpostavki vidite u Tabchnick i Fidell (2007, 4. poglavlje). Dalje razmatranje posledica narušavanja tih pretpostavki videti u knjigama Stevens (1996, 6. poglavlje) i Glass, Peckham i Sanders (1972).
Nivo merenja
Za sve parametarske pristupe pretpostavka je da se zavisna promenljiva meri na intervalnoj skali (pa rastojanja između brojčanih vrednosti odgovaraju rastojanjima između obeležja koja se mere). Dakle, upotrebljava se neprekidna skala, a ne diskretne kategorije (nekategorijske promenljive). Kad god je to moguće prilikom projektovanja istraživanja, pokušajte da upotrebite neprekidne mere zavisne promenljive, a ne kategorijske. Tako stičete mogućnost upotrebe većeg broja tehnika analize podataka.
Slučajnost uzorkovanja
Parametarske tehnike obrađene u 11., 12., 13. i 14. lekciji zasnivaju se na pretpostavci da su rezultati dobijeni iz slučajnog uzorka populacije. U stvarnim istraživanjima ta pretpostavka često nije zadovoljena.
Nezavisnost opservacija
Opservacije od kojih se sastoje podaci moraju biti uzajamno nezavisne, tj. ni na jednu opservaciju ili merenje ne sme uticati nijedna druga opservacija ili merenje. Kršenje ove pretpostavke ima vrlo ozbiljne posledice; raspravu videti u knjizi Stevens (1996, str. 238). U brojnim istraživačkim situacijama, krši se pretpostavka o nezavisnosti. U nastavku su dati primeri takvih studija (preuzete iz knjiga koje su napisali Stevens, 1996, str. 239; i Gravetter and Wallnau, 2004, str. 251):
- istraživanje učinka studenata koji rade u parovima ili malim grupama. Ponašanje svakog člana grupe utiče na sve ostale članove, čime se krši pretpostavka o nezavisnosti;
- istraživanje navika i preferencija dece u vezi s gledanjem TV-a, kada su deca iz iste porodice. Ponašanje jednog deteta u porodici (koje, recimo, gleda program A) najčešće utiče na svu ostalu decu iz te porodice, zato opservacije nisu nezavisne i
- istraživanje metoda poučavanja u učionici i njihovog uticaja na ponašanje i performanse studenata. Prisustvo malog broja problematičnih studenata može uticati na sve ostale; zato merenja ponašanja i performansi pojedinaca nisu nezavisna.
Treba sumnjati na svaku situaciju gde se opservacije ili merenja prikupljaju u grupnom okruženju ili su učesnici podvrgnuti nekom obliku međusobne interakcije. Kada budete projektovali istraživanje, pokušajte da obezbedite nezavisnost svih opservacija. Ako sumnjate da je ova pretpostavka narušena, Stevens (1996, str. 241) preporučuje da zadate strožu vrednost alfa (npr. p < 0,01).
Za svaku situaciju u kojoj se opservacije ili merenja prikupljaju u grupnom okruženju ili su učesnici podvrgnuti nekom obliku interakcije, mogu biti potrebne specifičnije tehnike, kao što je modelovanje u više nivoa (hijerarhijsko). Taj pristup je sada uobičajen u istraživanjima koja obuhvataju decu u učionici, u školama, u gradovima; ili studije s pacijentima, različitim medicinskim specijalistima, u ordinaciji/kancelariji, u gradu ili zemlji. Više o tome videti u 15. poglavlju knjige autorki Tabachnick i Fidell (2007).
Normalnost raspodele
Parametarske tehnike daju tačne rezultate samo kada su populacije iz kojih su uzorci uzeti normalno raspodeljene. U mnogim istraživanjima (naročito u društvenim naukama) vrednosti zavisne promenljive nisu normalo raspodeljene. Srećom, većina tehnika je prilično robusna, tj. narušavanje ove pretpostavke prouzrokuje malu netačnost rezultata. Kada su uzorci dovoljno veliki (npr. preko 30 opservacija), kršenje ove pretpostavke ne bi trebalo da prouzrokuje veće probleme. To je pravilo centralne granične teoreme. Raspodela rezultata za svaku grupu može se proveriti pregledom histograma koji se crtaju pomoću SPSS-ovog menija Graphs (videti 5. lekciju). Podrobniji opis tog procesa videti u knjizi koju su napisale Tabachnick i Fidell (2007, 4. poglavlje).
Homogenost varijanse
Parametarske tehnike koje će biti obrađene u narednim lekcijama temelje se na pretpostavci da su uzorci dobijeni iz populacija jednakih varijansi. To znači da je promenljivost rezultata u svim grupama jednaka. Za ispitivanje te homogenosti u sklopu t-testova i analiza varijansi, SPSS obavlja Levene-ov test jednakosti varijanse. Njegovi rezultati su deo SPSS-ovog izlaza za te tehnike. Budite pažljivi u tumačenju rezultata tog testa: nadate se da pokazatelj nije značajan (tj. da mu je značajnost veća od 0,05; p > 0,05). Kada dobijete značajnost manju od 0,05, to znači da varijanse dveju grupa nisu jednake i da ne važi pretpostavka o homogenosti varijanse. Ne paničite kada vam se to dogodi. Analiza varijanse je prilično neosetljiva na narušavanje te pretpostavke ukoliko su veličine grupe približno slične (npr. najveća/najmanja =1,5; Stevens, 1996, str. 249). U t-testovima dobijate dva niza rezultata, jedan za situacije u kojima pretpostavka nije narušena, a drugi za one kada jeste. U tom slučaju samo upotrebite onaj skup rezultata koji odgovara podacima.
T-testovi i analize varijansi služe za ispitivanje hipoteza. U toj vrsti analiza uvek je moguće doneti pogrešan zaključak. Mogu se napraviti dve različite greške. Kada odbacimo nultu hipotezu koja je u stvari tačna, radi se o grešci prve vrste. To se dešava kada zaključujemo da između grupa postoji razlika, o ona zapravo ne postoji. Verovatnoću te greške minimiziramo tako što izaberemo malu vrednost alfa; najčešće se koriste vrednosti 0,05 ili 0,01, tj. svesno rizikujemo da jedanput u 20 odnosno 100 slučajeva odbacimo nultu hipotezu (o nepostojanju razlike) kada je tačna.
U ispitivanju (verifikaciji) hipoteza može se napraviti i druga vrsta greške, kada ne odbacimo pogrešnu nultu hipotezu (tj. kada zaključimo da između grupa ne postoji razlika, a ona zapravo postoji). Nažalost, te dve greške su obrnuto srazmerne. Što više smanjujemo verovatnoću greške I vrste, povećavamo verovatnoću da ćemo napraviti grešku II vrste.
Idealno bi bilo da se pomoću upotrebljenih testova tačno utvrdi postoji li zaista razlika između grupa. To je tzv. moć testa, tj. verovatnoća da se otkrije postojeća razlika, odnosno da se ne napravi greška II vrste. Testovi se razlikuju po svojoj moći; recimo, kada su njihove osnovne pretpostavke zadovoljene, parametarski testovi (kao što su t-testovi, analiza varijanse, itd.) potencijalno su moćniji od neparametarskih testova. Međutim, na moć testa u datoj situaciji utiču i drugi činioci:
- veličina uzorka;
- veličina uticaja istraživane razlike između grupa, tj. uticaja nezavisne promenljive i
- alfa nivo (rizik greške I vrste) koji je zadao istraživač (npr. 0,05/0,01).
Moć testa se jako menja u zavisnosti od veličine uzorka upotrebljenog u studiji. Stevens (1996) tvrdi da "moć ne prestavlja problem" (str. 6) kada je uzorak veliki (npr. 100 ili više učesnika). Međutim, u istraživanjima na malim uzorcima (npr. n = 20) morate biti svesni mogućnosti da neznačajan rezultat može biti posledica nedovoljne moći testa. Stevens (1996) predlaže da se za male grupe po potrebi poveća alfa (rizik greške I vrste), npr. na 0,10 ili 0,15 umesto uobičajenih 0,05.
Postoje i tabele (videti Cohen, 1988) u kojima se može očitati veličina uzorka potrebna za određenu (dovoljnu moć testa), za datu veličinu uticaja razlike koju želite da otkrijete. Sve više je i softverskih programa koji to umeju da izračunaju (npr. G*Power, koji se može preuzeti sa sledećeg linka: https://stats.idre.ucla.edu/other/gpower/).
I u nekim SPSS procedurama izračunava se moć obavljenog testa, pri čemu se vodi računa o veličini uticaja razlike i veličini uzorka. Idealno bi bilo da imate 80 procenata šanse da otkrijete postojanje veze. Kada dobijete neznačajan rezultat i imate veoma mali uzorak, trebalo bi da pogledate moć upotrebljenog testa. Uz moć testa manju od 0,80 (80 procenata šanse da otkrijete postojeću razliku), treba pažljivo protumačiti razlog neznačajnosti rezultata. Ona može biti posledica nedovoljne moći testa, a ne nepostojanja razlike između grupa. Analiza moći pokazuje koliko poverenja treba imati u rezultate kada se ne odbaci nultu hipoteza o jednakosti grupa. Što je veća moć testa, to više tada treba biti uveren da stvarna razlika između grupa ne postoji.
Analizom varijanse utvrđujete da li postoje značajne razlike između raznih grupa ili okolnosti. Katkada će vas zanimati da li su grupe kao celina razlikuju (da li nezavisna promenljiva na neki način utiče na vrednosti zavisne promenljive). U drugim istraživačkim kontekstima usredsredićete se više na ispitivanje razlika između pojedinih, za razliku od svih mogućih, grupa. Vodite računa o toj razlici, pošto se za svaku od tih namena koristi drugačija analiza.
Planirana (ili a priori) poređenja služe za ispitivanje konkretnih hipoteza (obično izvučenih iz teorije ili prethodnih istraživanja) u vezi s razlikama unutar određenog podskupa grupa (npr. da li se grupe 1 i 3 značajno razlikuju?). Ta poređenja treba specificirati (isplanirati) pre nego što analizirate podatke, umesto da tragate po rezultatima u nadi da ćete naći nešto zanimljivo!
Ukoliko nameravate da specificirate mnogo različitih, ali istovremenih poređenja, moraćete postupiti pažljivo. Planirana poređenja ne uklanjaju povećani rizik od greške I vrste, koji je posledica velikog broja paralelnih hipoteza koje se ispituju. Greška I vrste znači odbaciti nultu hipotezu (npr. da nema razlike između grupa) koja je u stvari tačna. Drugim rečima, povećan je rizik da ćete misliti da ste otkrili značajan rezultat (razliku), a on je zapravo sasvim slučajan. Kada istražujete veliki broj razlika, bezbednije je drugačiji pristup, tj. naknadna (post-hoc ili a posteriori) poređenja, koja štite od greške I vrste.
Treća mogućnost je da na alfa nivo (rizik greške I vrste) koji ćete upotrebiti za procenu statističke značajnosti, primenite tzv. Bonferonijevo prilagođavanje. To znači zadati stroži alfa nivo za svako poređenje, da bi alfa u svim testovima zajedno ostao na razumnom nivou. To se postiže deljenjem alfa nivoa (najčešće 0,05) brojem poređenja koje nameravate da obavite; zatim se ta nova vrednost koristi kao zahtevani alfa nivo. Primera radi, za tri nameravana poređenja novi alfa nivo bio bi 0,05 podeljeno s 3, što je jednako 0,017. Raspravu o tome vidite u Tabachnick i Fidell (2007, str. 52).
Naknadna (post-hoc ili a posteriori) poređenja upotrebljavaju se kada želite da obavite ceo niz poređenja, tj. istražite razlike između svih mogućih grupa ili uslova u studiji. Ukoliko odaberete taj pristup, analiza treba da se sastoji od dva koraka. Prvo se izračunava F pokazatelj koji kazuje ima li značajnih razlika između grupa u projektu. Ako je ukupan F pokazatelj značajan (što ukazuje da postoji razlika između grupa), možete nastaviti i obaviti dodatne testove za identifikaciju tih razlika (npr. da li se Grupa 1 razlikuje od Grupe 2 ili Grupe 3, da li se razlikuju Grupa 2 i Grupa 3).
Naknadna poređenja štite od moguće greške I vrste kao posledice velikog broja različitih poređenja. To se postiže zadavanjem strožih kriterijuma za značajnost, koju je utoliko teže postići. Kod malih uzoraka to ume da bude problem, zato što je ponekad vrlo teško dobiti značajan rezultat, čak i kada je vidljiva razlika u rezultatima između grupa veoma velika.
Postoje i brojni naknadni testovi koji se razlikuju po svojoj prirodi i strogosti. Razlikuju se i pretpostavke na kojima se zasnivaju. U nekima se pretpostavlja da su varijanse dve grupe jednake (npr. Tukey); u drugima se ne pretpostavlja jednakost varijansi (npr. Dunnettov C test). Među najčešće upotrebljavanim naknadnim testovima su Tukejev test "zaista značajne različitosti" (engl. Honestly Significant Different, HSD) i Šefeov (Scheffe) test. Od ta dva, Šefeov test je bezbednija metoda za smanjenje rizika od greške I vrste. Međutim, to se plaća u moći. Tim testom je teže (manje verovatno) otkriti stvarno postojeću razliku između grupa.
Sve tehnike razmotrene kako u ovoj , tako i u narednim lekcijama pokazuju da li je razlika između grupa statistički značajna (tj. neslučajna). Za većinu istraživača i studenata nastupi trenutak uzbuđenja kada utvrde da su njihovi rezultati statistički značajni! Međutim, istraživanje znači više od dobijanja statističke značajnosti. Verovatnoća ne pokazuje stepen povezanosti promenljivih (jačinu veze). Kada su izračunate za velike uzorke, čak i vrlo male razlike između grupa postaju statistički značajne. To ne znači da je ta razlika dovoljno velika da bi imala ikakvu praktičnu ili teorijsku važnost.
Jedan od načina da ocenite važnost svojih rezultata jeste da izračunate veličinu uticaja (engl. effect size), tj. jačinu veze između promenljivih. To je skup pokazatelja koji pokazuje relativnu veličinu razlika između srednjih vrednosti ili iznos ukupne varijanse u zavisnoj promenljivoj koji se može predvideti na osnovu poznavanja vrednosti nezavisne promenljive (Tabachnick & Fidell, 2007, str. 54).
Ima više pokazatelja veličine uticaja. Za poređenje grupa najčešće se upotrebljavaju pokazatelji parcijalni eta kvadrat i Koenov d. SPSS izračunava parcijalni eta kvadrat u sklopu analize varijanse, ali ne i u sklopu t-testova; no, to je lako izračunati na osnovu drugih njegovih rezultata.
Pokazatelj veličine uticaja parcijalni eta kvadrat srazmeran je delu varijanse zavisne promenljive koji je objašnjen nezavisnom promenljivom. Može imati vrednosti u opsegu od 0 do 1. S druge strane, Koenov d predstavlja razliku između grupa izraženu brojem standardnih odstupanja. Pazite da ne pobrkate te pokazatelje kada budete tumačili jačinu veze. Adresa Web lokacije na kojoj se brzo i lako mogu izračunati oba spomenuta pokazatelja veličine uticaja glasi: https://effect-size-calculator.herokuapp.com/.
Cohen (1988, str. 22) predložio je sledeće smernice za tumačenje veličine uticaja (kada se ocenjuje istraživanje koje obuhvata poređenje grupa). Koenova preporuka se odnosi na pokazatelj et kvadrat, ali se može primeniti i na tumačenje pokazatelja parcijalni eta kvadrat. Formula za parcijalni ima neznatno drugačiji imenilac. Više o tome pročitajte u knjizi autorki Tabachnick i Fidell, 2007, str. 55.

Slika-2 Utvrđivanje veličine uticaja na osnovu pokazatelja parcijalni eta kvadrat i Koenov d
Vodite računa o tome da Koen daje drugačije smernice za korelacione projekte (obrađene u 7., 8. i 9. lekciji). Gornje vrednosti važe za poređenja grupa.
Preuzeto iz: Pallant, J. (2011), SPSS: priručnik za preživljavanje (prevod 4. izdanja), Beograd: Mikro knjiga
Kada se radi istraživanje, pogotovo ono s ljudima, retko se za svaki ispitivani slučaj dobijaju potpuni podaci. Uvek treba pregledati da li u datoteci nedostaju neki podaci. Pokrenite funkciju Descriptives i za svaku promenljivu utvrdite koliki procenat podataka nedostaje. Kada pronađete promenljivu kojoj neočekivano nedostaje mnogo podataka, zapitajte se koji je razlog tome i da li podaci nedostaju nasumično ili tu možete uočiti neku pravilnost (npr. mnoge žene nisu odgovorile na pitanje o svojoj starosti). SPSS ima proceduru Missing Value Analysis koja olakšava pronalaženje pravilnosti u nedostajućim podacima (videti poslednju opciju u meniju Analyze). Više o tome pročitajte u 4. poglavlju knjige autorki Tabachnick i Fidell, 2007.
Kada dođe vreme za statističke analize, moraćete da razmislite i odlučite šta ćete preuzeti u vezi s nedostajućim podacima. U mnogim SPSS-ovim statističkim postupcima, preko dugmeta Options pristupate mogućim načinima tretiranja nedostajućih podataka. Birajte pažljivo, jer izbor može značajno uticati na rezultate, naročito ako prilažete spisak promenljivih i iste analize ponavljate za sve promenljive (npr. korelacije između grupe promenljivih, t-testovi niza zavisnih promenljivih).
- Opcija Exclude case listwise znači da će biti analizirani samo slučajevi u kojima za sve promenljive navedene u polju Variables postoje svi podaci. Svaki ispitivani slučaj za koji nedostaje makar i delić podataka, uopšte neće biti analiziran. To može znatno i nepotrebno ograničiti veličinu uzorka;
- Opcija Exclude cases pairwise znači da će slučaj (osoba) biti isključen samo iz onih analiza za koje mu nedostaje neki neophodan podatak. Dakle, i takvi slučajevi će biti analizirani kad god je to moguće, tj. kad god postoje podaci potrebni za datu analizu i
- Opcija Replace with mean, dostupna u nekim SPSS-ovim statističkim postupcima (npr. u višestrukoj regresiji), znači da će biti izračunata srednja vrednost svih promenljivih i da će njome biti zamenjeni podaci koji nedostaju. Ovu opciju nikada ne bi trebalo da koristite, pošto može znatno da iskrivi rezultate analize, naročito onda kada nedostaje mnogo podataka.
Kada god sprovodite neki statistički postupak, pritisnite dugme Options i proverite koja je od navedenih opcija potvrđena (jer se podrazumeva opcija menija u zavisnosti od postupka). Ako nemate jak razlog da postupite drugačije, preporučljivo je da slučajeve isključite samo iz onih analiza za koje im nedostaju podaci (pairwise). Jedina situacija kada bi vam moglo zatrebati da analize ograničite samo na slučajeve koji imaju podatke za sve promenljive (listwise) jeste onda kada treba razmotriti samo podskup slučajeva koji daje potpun skup rezultata.
