- Hi-kvadrat test za ispitivanje kvaliteta podudaranja
- Postupak za obavljanje hi-kvadrat test kvaliteta podudaranja
- Tumačenje i predstavljanje rezultata hi-kvadrat testa podudaranja
- Hi-kvadrat test nezavisnosti
- Postupak za obavljanje hi-kvadrat testa nezavisnosti - I deo
- Postupak za obavljanje hi-kvadrat testa nezavisnosti - II deo
- Tumačenje rezultata hi-kvadrat testa nezavisnosti - I deo
- Tumačenje rezultata hi-kvadrat testa nezavisnosti - II deo
- Tumačenje rezultata hi-kvadrat testa nezavisnosti - III deo
- Hi-kvadrat test nezavisnosti - video
Postoji više testova zasnovanih na hi-kvadrat statistici, a svi su namenjeni za kategorijske podatke. U nastavku ove lekcije će biti objašnjeni hi-kvadrat test za ispitivanje kvaliteta podudaranja i hi-kvadrat test nezavisnosti. Opširniji prikaz testa hi-kvadrat dat je u 17. poglavlju knjige autora Gravetter i Wallnau (2004).
Hi-kvadrat test za ispitivanje kvaliteta podudaranja
Ovaj test, koji se naziva i hi-kvadrat test jednog uzorka, često se upotrebljava za poređenje proporcije slučajeva iz određenog uzorka s hipotetičkim vrednostima ili onima prethodno dobijenim u nekoj poredbenoj populaciji. Dovoljno je da datoteka s podacima sadrži samo jednu kategorijsku promenljivu i određenu proporciju s kojom želite da uporedite dobijene rezultate. Može se ispitati hipoteza da nema razlike u proporciji kategorija (50%/50%) ili određena proporcija dobijena u nekoj prethodnoj studiji.
Primer istraživačkog pitanja: Istražiće se da li je procentualni udeo pušača u populaciji opisanoj u datoteci survey3ED.sav ekvivalentan onome (20%) navedenom u literaturi prethodno objavljene velike austrijske studije.
Šta vam treba:
- jedna kategorijska promenljiva sa dve ili više kategorija: pušač (Da/Ne) i
- hipotetička proporcija (20% pušača; 80% nepušača ili 0,2/0,8).
Da biste pratili ovaj primer, otvorite datoteku survey4ED.sav.
- Otvorite meni Analyze, pritisnite njegovu stavku No-parametric tests, pa Legacy Dialogs i zatim Chi-Square;
- Pritisnite kategorijsku promenljivu smoke (tj. pušač), pa pritisnite strelicu da biste promenljivu prebacili u polje Test Variable List;
- U odeljku Expected Values pritisnite opciju Values. U polje Values treba da upišete dva broja. Prvi broj (0,2) odgovara očekivanoj proporciji prve šifrovane vrednosti te promenljive (1 = da, pušač). Pritisnite dugme Add. Upišite drugi broj (0,8), što je očekivana proporcija druge šifrovane vrednosti te promenljive (2 = ne, nepušač). Pritisnite dugme Add. Ukoliko promenljiva ima više od dve moguće vrednosti, za svaku od njih treba upisati odgovarajuću proporciju;
- Pritisnite OK.
Evo i kako izgledaju rezultati tog postupka:
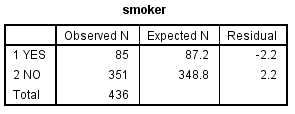
Slika-1 Opažane učestalosti (frekvencije)

Slika-2 Test Statistics
Tumačenje rezultata
U prvoj tabeli date su opažane učestalosti (frekvencije) iz tekuće datoteke s podacima; vidimo da su pušači njih 85 od ukupno 436 (19,5%). U koloni Expected N date su učestalosti očekivane na osnovu prethodno zadate proporcije (20%). U ovom slučaju, očekivano je da bude 87 pušača, a opažano je 85.
U tabeli Test Statistics dati su rezultati SPSS-ovog testa Chi-Square, koji poredi očekivane i opažane vrednosti. U ovom slučaju, razlika između njih je vrlo mala, a nije ni statistički značajna (Sig. = 0,79; p > 0,05).
Predstavljanje rezultata
Treba navesti vrednost hi-kvadrat, broj stepeni slobode (engl. degrees od freedom, df) i vrednost p (prikazana kao Asymp. Sig.).
Hi kvadrat test podudaranja pokazuje da se proporcija pušača u tekućem uzorku (19,5%), ne razlikuje mnogo od vrednosti 20% dobijenoj u prethodnoj austrijskoj studiji, X2 (1, n = 436) = 0,07, p < 0,79.
Više puta je naglašeno da se u marketinškim istraživanjima često ispitanicima postavljaju pitanja (ili se beleže karakteristike ispitanika) koja su u formi kategorijskih obeležja. Videli smo da se u tim slučajevima koriste tabele frekvencija i unakrsno tabeliranje (engl. cross-tabulation), kao i hi-kvadrat analiza za poređenje proporcija određenog obeležja za jedan ili više osnovnih skupova. Naime, hi-kvadrat analizom se pored testiranja oblika rasporeda, testira i postojanje neke veze - asocijacije između kategorijskih promenljivih.
Drugim rečima, hi-kvadrat testom nezavisnosti (hi-kvadrat testom statistika) se istražuje veza između dve kategorijske promenljive. Svaka od njih može imati dve ili više kategorija. Test poredi učestalosti ili proporcije slučajeva opažane u svakoj od kategorija, s vrednostima koje bi bile očekivane da između dve merene promenljive nema nikakve veze. Tačnije, nulta hipoteza za ovaj test je da ne postoji veza između kategorijskih promenljivih, tj. da su posmatrane učestalosti (frekvencije) jednake očekivanim frekvencijama. Ovaj test se zasniva na unakrsnoj tabeli, tj. u tabeli u kojoj su kategorije jedne promenljive ukrštene s kategorijama druge (npr. muškarci/žene; pušač/nepušač); svaka ćelija unakrsne tabele sadrži po jednu kombinaciju kategorija posmatranih promenljivih.
Kada SPSS naiđe na tabelu 2 sa 2 (po dve kategorije u svakoj promenljivoj), rezultat hi-kvadrat testa obuhvata i jednu dodatnu "korekciju neprekidnosti prema Jejtsu" (engl. Yates' Correction for Continuity). Ona bi trebalo da kompenzuje (po mišljenju nekih autora) precenjenu vrednost hi-kvadrat koja se dobija u tabeli 2 sa 2.
U sledećem postupku, na primeru datoteke survey4ED.sav biće pokazano kako se upotrebljava hi-kvadrat test za projekat 2 sa 2. Kada studija obuhvata promenljive s više od dve kategorije (npr. 2 sa 3, 4 sa 4), videćete da se izlaz iz SPSS-a neznatno razlikuje.
Primer istraživačkog pitanja: Pitanje se može formulisati na više načina - postoji li veza (zavisnost) između pola i pušačkog ponašanja? Da li su muškarci češće pušači od žena? Da li je proporcija muškaraca jednaka toj proporciji kod žena?
Šta vam treba: Dve kategorijske promenljive sa po dve ili više kategorija - pol (Muškarac/Žena) i pušač (Da/Ne).
Dodatne pretpostavke: Najmanja očekivana učestalost u svim ćelijama trebalo bi da bude 5 ili više. Neki autori predlažu blaže kriterijume: najmanje 80 procenata ćelija trebalo bi da imaju očekivane učestalosti 5 ili više. Za tabelu 2 sa 2, preporučuje se da očekivana učestalost bude najmanje 10. Kada tabela 2 sa 2 ne zadovoljava ovu pretpostavku, umesto vrednosti hi-kvadrat treba upotrebiti Fišerov "tačan pokazatelj verovatnoće" (engl. Fisher's Exact Probability Test). Njega automatski generiše SPSS i navodi u sklopu rezultata hi-kvadrat testa.
Da biste pratili ovaj primer, otvorite datoteku survey4ED.sav.
- Otvorite meni Analyze, pritisnite stavku Descriptive Statistics, zatim Crosstabs;
- Pritisnite onu promenljivu (npr. sex/pol) čije će kategorije zauzimati redove tabele; pritisnite strelicu da biste izabranu promenljivu prebacili u polje Row(s);
- Pritisnite onu promenljivu (npr. smoke/pušač) čije će kategorije zauzimati kolone tabele, pa pritisnite strelicu da biste izabranu promenljivu prebacili u polje Column(s);
- Pritisnite dugme Statistics. Potvrdite polje Chi-Square i Phi and Cramer's V. Pritisnite Continue.
- Pritisnite dugme Cells. U polju Counts pritisnite Observed. U odeljku Percentage potvrdite polja Row, Column i Total i
- Pritisnite Continue i zatim OK.
Sledi deo rezultata opisanog postupka za tabelu 2 sa 2. Rezultat se malo razlikuje za promenljive s više od dve kategorije, ali u njemu i dalje treba tražiti iste ključne podatke.
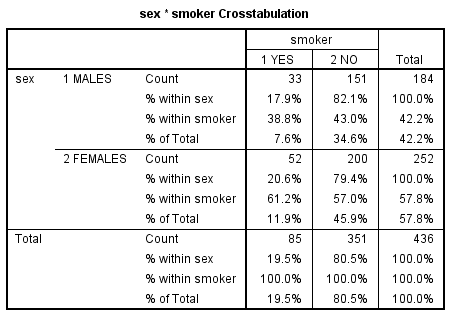
Slika-3 sex * smoker Crosstabulation
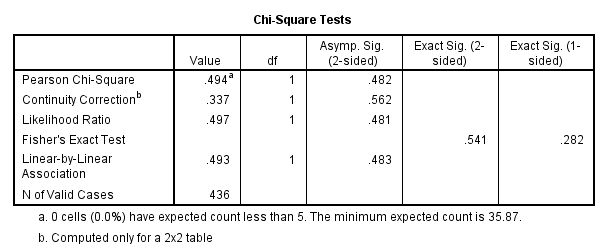
Slika-4 Chi-Square Test
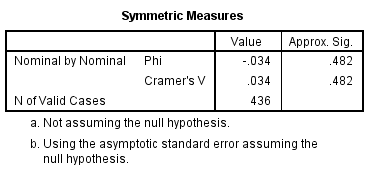
Slika-5 Symmetric Measures
Pretpostavke
Najpre treba proveriti da li je prekršena jedna od pretpostavki testa hi-kvadrat u pogledu najmanje očekivane ćelijske učestalosti, koja bi trebalo da bude 5 ili više (ili da najmanje 80 procenata ćelija ima očekivane učestalosti 5 ili više). Ta informacija je data u fusnoti ispod tabele Chi-Square Tests. U fusnoti b u primeru kaže se "0 cells (,0%) have expected count less than 5. The minimum expected count is 35,87". To znači da nismo prekršili pretpostavku, pošto su očekivane učestalosti u svim ćelijama veće od 5 (u našem primeru, veće od 35,87).
Hi-kvadrat testovi
U rezultatima najviše nas zanima vrednost hi-kvadrat statistike (engl. Pearson Chi-Square), data u tabeli Chi-Square Tests. Međutim, kada se ima tabela 2 sa 2 (tj. kada svaka promenljiva ima samo dve kategorije), treba upotrebiti vrednost u drugom redu tabele (Continuity Correction). To je tzv. Jejtsova korekcija (engl. Yates' Correction for Continuity); ona kompenzuje precenjenu vrednost hi-kvadrat koja je posledica malog broja dimenzija tabele 2 sa 2. U gornjem primeru, korigovana vrednost iznosi 0,337, uz značajnost 0,56 (datu u koloni Asymp. Sig. (2-sided)). Da bi rezultat bio značajan, veličina Sig. treba da je 0,05 ili manja. U ovom primeru, vrednost 0,56 je (11 puta) veća od alfa vrednosti 0,05, pa možemo zaključiti da naš rezultat nije značajan. To znači da se proporcija muškaraca koji puše ne razlikuje od proporcije žena koje puše. Drugim rečima, nema nikakve veze između pušačkog statusa i pola. Time je potvrđena nulta hipoteza.
Unakrsno tabeliranje
Procenat pušača svakog pola može se očitati u zbirnim informacijama datim u tabeli sex * smok Crosstabulation. S toliko informacija naguranih u svaku ćeliju, ova tabela vas može zbuniti. Da biste saznali koji procenat muškaraca su pušači, pročitajte prvi red tabele koji se odnosi na muškarce. U ovom slučaju, gledamo šta piše u nastavku % within sex. U ovom primeru , 17,9% procenata muškaraca su pušači i 82,1 procenata nepušači; 20,6 procenata žena je pušača i 79,4 procenata nepušača. Kako biste bili sigurni da čitate ispravne vrednosti, proverite da li zbir te dve procentualne vrednosti iznosi 100%.
Da nas zanima procenat celog uzorka koji spada u pušače, prešli bismo naniže u poslednji red, koji sabira rezultate za oba pola. U ovom slučaju, pogledali bismo šta piše u redu % of Total. Prema tim rezultatima, 19,5 procenata uzorka puši, a 80,5 procenata ne puši.
Veličina uticaja
U proceduri Crosstabs izračunava se više pokazatelja veličine uticaja (tj. jačine veze između promenljivih). Za tabele 2 sa 2, najčešće se koristi koeficijent fi (phi coefficient), što je koeficijent korelacije u opsegu od 0 do 1, pri čemu veći broj pokazuje jaču vezu između dve promenljive. U ovom primeru, koeficijent fi (prikazan u tabeli Symmetric Measures) iznosi -0,034, što se smatra vrlo malim uticajem po Koenovom (1988) kriterijumu od 0,10 za mali, 0,30 za srednji i 0,50 za veliki uticaj.
Za tabele veće od 2 sa 2, u izveštaj treba staviti Kramerov pokazatelj V (Cramer's V), koji uzima u obzir broj stepeni slobode. Za ocenu veličine uticaja kod većih tabela koriste se malo drugačiji kriterijumi. Da biste utvrdili koji kriterijum da upotrebite, najpre oduzmite 1 od broja kategorija u rednoj promenljivoj (R-1), a zatim oduzmite 1 od broja kategorija u kolonskoj promenljivoj (K-1). Od ta dva broja, zadržite onaj manji.
Za R-1 ili K-1 jednako 1 (dve kategorije): mali = 0,01, srednji = 0,30 i veliki = 0,50.
Za bilo R-1 bilo K-1 jednako 2 (tri kategorije): mali = 0,07, srednji = 0,21 i veliki = 0,35.
Za bilo R-1 bilo K-1 jednako 3 (četiri kategorije): mali = 0,06, srednji = 0,17 i veliki = 0,29.
Više o pokazateljima koeficijent fi i Kramerov V pročitajte u knjizi autor Gravetter i Wallnau (2004, str. 605).
Rezultate ove analize mogli biste predstaviti ovako: Hi-kvadrat test nezavisnosti (uz korekciju neprekidnosti prema Jejtsu) nije pokazao značajnu vezu između pola i pušačkog statusa, X2 (1, n = 436) = 0,34, p = 0,56, fi = -0,034.
Preuzeto iz: Pallant, J. (2011), SPSS: priručnik za preživljavanje (prevod 4. izdanja), Beograd: Mikro knjiga
