Pokazna vežba

Zadatak 1(5 minuta)
Zadatak 2 (10 minuta)
Zadatak 3 (15 minuta)
Zadatak 4 (15 minuta)
Zadatak 5 (5 minuta)
Zadatak 6 (5 minuta)
Zadatak 7 (5 minuta)
Zadatak 8 (10 minuta)
Zadatak 9 (10 minuta)
Zadatak 10 (5 minuta)
Zadatak 11 (10 minuta)
Video klip
Zadatak 12 – 1. deo (20 minuta)
Zadatak 12 – 2. deo
Zadatak 13 – 1. deo (20 minuta)
Zadatak 13 – 2. deo

09

Zadatak 1(5 minuta)

Određivanje domena.

Odrediti domen funkcije:

$f (x, y) = \frac{2}{x - y} .$

Rešenje:

Domen zadate funkcije je skup svih tačaka u ravni $ℝ^{2}$ koje zadovoljavaju uslov:

$x - y \neq 0$

tj. uslov se može zapisati kao

$x \neq y$

Skup tačaka koje ne zadovoljavaju navedeni uslov čini pravu $y = x .$ Dakle, tada imamo:

$D = \{(x, y) \in ℝ^{2}| - \infty \leq x \leq \infty, y \neq x\} .$

Zadatak 2 (10 minuta)

Određivanje domena funkcije dve promenljive

Odrediti domen funkcije

$f (x, y) = \sqrt{1 - x^{2} - y^{2}} .$

Rešenje: Domen zadate funkcije je skup svih tačaka u ravni $ℝ^{2}$ koje zadovoljavaju uslov da je potkorena veličina $1 - x^{2} - y^{2} \geq 0$ .

Ovaj uslov se može zapisati kao:

$x^{2} + y^{2} \leq 1 .$

Skup tačaka koje zadovoljavaju navedeni uslov čini kružnicu $x^{2} + y^{2} = 1$ i njenu unutrašnjost tj. $D = \{(x, y) \in ℝ^{2}| x^{2} + y^{2} \leq 1\}$

Skup tačaka u ravni ograničen nekom krivom, pravom i krivom, nekim krivima ili pravama i krivima se u najvećem broju slučajeva može predstaviti i tako što se jednoj od promenljivih u jednačini te krive (ili krivih) i prave (ili pravih) odredete brojne granice u kojima se kreće, a drugoj promenljivoj su, tada, granice u kojima se kreće funkcionalne tj. zavise od ove prve pormenljive. Ponekad je posmatrani skup tačaka u ravni dobijen presekom više krivih ili pravih, pa se u tom slučaju posmatrani skupa tačaka u ravni može predstaviti kao unija više disjunktnih skupova skupova čija unija čini početni skup tačaka. Ovo razbijanje se vrši zbog toga što se se granice početnog skupa tačaka menjaju, jer su dobijene presekom više pravih ili krivih.

U ovom primeru to možemo zapisati na sledeći način (videti sliku):

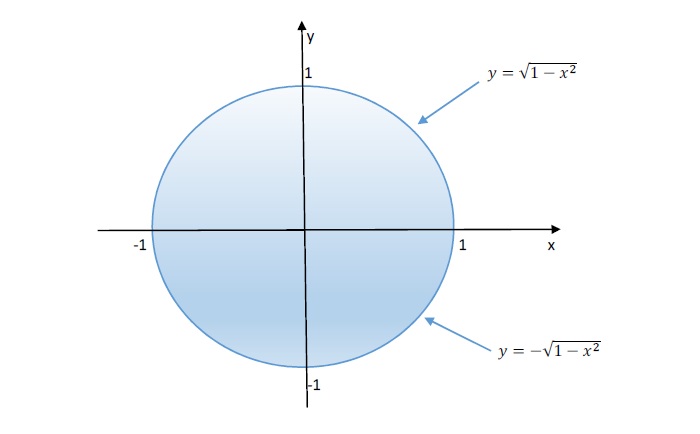
$D = \{(x, y) \in ℝ^{2}| - 1 \leq x \leq 1, - \sqrt{1 - x^{2}} \leq y \leq \sqrt{1 - x^{2}}\} .$

Slika-1 Grafičko predstavljanje domena funkcije [Izvor: Autor].

Svakako, predstavljanje je moglo ići tako što se $y$ predstavlja kao u brojnim granicama, a $x$ u funkcionalnim. Tada imamo:

$D = \{(x, y) \in ℝ^{2}| - 1 \leq y \leq 1, - \sqrt{1 - y^{2}} \leq x \leq \sqrt{1 - y^{2}}\} .$

Zadatak 3 (15 minuta)

Određivanje domena funkcije

Odrediti domen funkcije $$z = \sqrt{ \ln x + \ln y } . $$ $\textbf{ Rešenje. } $ Zbog logaritamske funkcije važi $ x > 0 $ i $ y > 0 , $ a zbog kvadratnog korena važi da je $ \ln x + \ln y \geq 0 , $ tj. $ \ln xy \geq 0 , $ tj. $ x y \geq 1 . $ Ukupno, imamo da je $ y \geq \frac1 x , $ za $ x > 0$ i $ y > 0 .$ Tada domen ove funkcije predstavlja skup $$ { \cal D } = \big \{ ( x , y ) \in \mathbb{ R } ^ 2 \mid y \geq \frac1 x \wedge x > 0 \wedge y > 0 \big\} . $$ Napomenimo da $ x y = 1 $ predstavlja jednačinu parabole čije su asimptote koordinatne ose u prvom i trećem kvadrantu. Na osnovu postavljenih uslova, domen funkcije predstavlja deo prvog kvadranta iznad parabole $y = \frac1 x , $ uključujući i nju kao graničnu liniju (videti sliku).

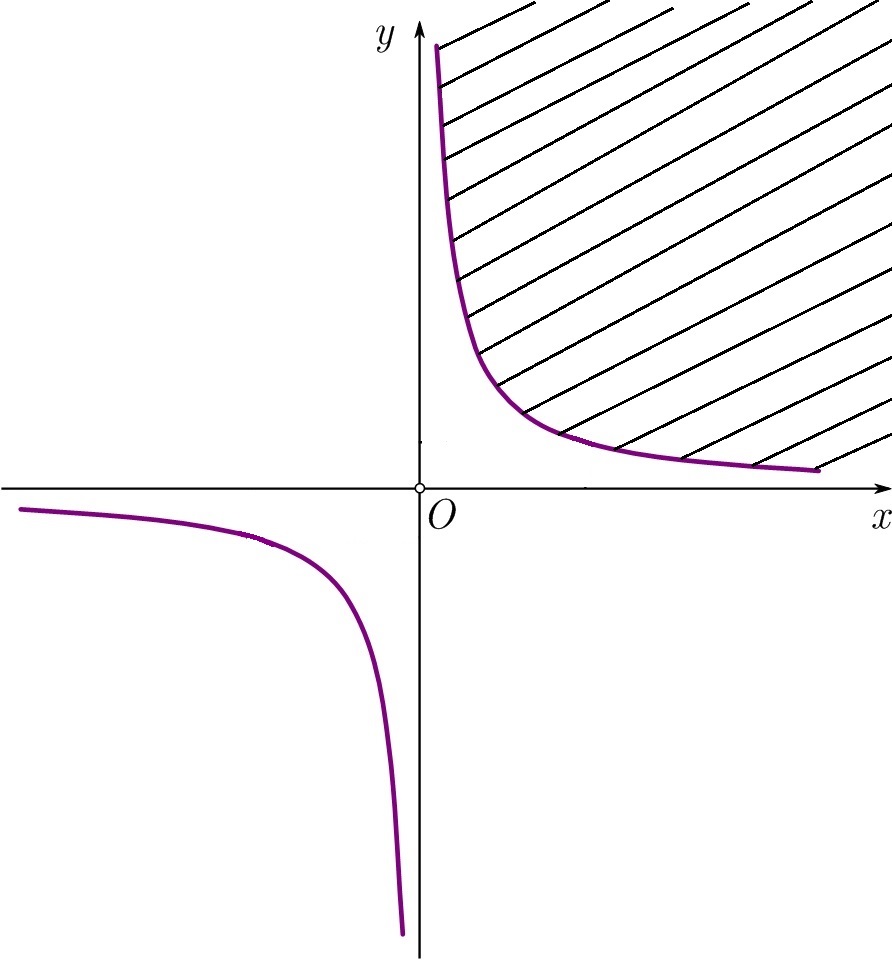
Slika-2 Domen funkcije $z = \sqrt{ \ln x + \ln y }$ [Izvor: Autor].

Odrediti domen funkcije $z=\dfrac{\arcsin(x^2+y^2-3)}{\ln(x-y)}.$

$\textbf{Rešenje. } $ Domen inverzne trinometrijske funkcije $y=\arcsin x$ je $-1\leq x\leq 1,$ pa je u našem slučaju $ - 1 \leq x ^ 2 + y ^ 2 - 3 \leq 1 , $ odnosno $ 2 \leq x ^ 2 + y ^ 2 \leq 4 . $ Dalje, zbog logaritamske funkcije imamo da je $ x - y > 0 , $ tj. $ x > y . $ Na kraju, važi da je $ \ln( x - y ) \not= 0 , $ tj. $ x - y \not= 1 $ odnosno $ y \not= x - 1 . $ Tada je domen ove funkcije skup $$ { \cal D } = \big\{ ( x , y ) \in \mathbb{ R } ^ 2 \mid 2 \leq x^2 + y^2 \leq 4 \wedge x > y \wedge y \not = x - 1 \big \} , $$ koji predstavlja deo ravni unutar kružnog prstena $ 2 \leq x ^ 2 + y ^ 2 \leq 4 $ (obojen plavom bojom na datoj slici), koji se nalazi ispod prave $ y = x $ (ne uključujući i nju), iz koga su izbačene tačke sa prave $ y = x - 1 . $

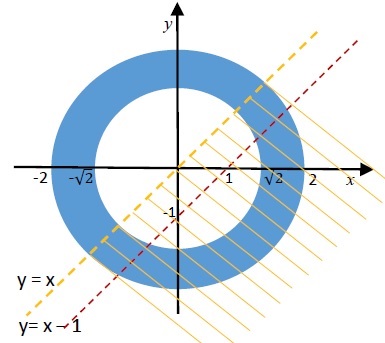
Slika-3 Domen funkcije $z=\dfrac{\arcsin(x^2+y^2-3)}{\ln(x-y)}$ [Izvor: Autor].

Zadatak 4 (15 minuta)

Ispitivanje postojanja granične vrednosti funkcije u određenoj tački.

Ispitati da li postoje sledeće granične vrednosti
a) $\lim\limits_{(x,y)\to(0,0)}\dfrac{xy}{x^2+y^2};$

b) $\lim\limits_{(x,y)\to(2,0)}\dfrac{\sin (xy)}{y};$

c) $\lim\limits_{(x,y)\to(-\infty,+\infty)}\dfrac{x^{3}+y^{3}}{x^{4}+y^{4}}.$

$ \textbf{ Rešenje. } $ a) Uvedimo smenu $x=\rho\cos\theta$ i $y=\rho\sin\theta,$ gde je $\rho>0$ i $\theta\in(0,2\pi].$ Tada, dobijamo da $\rho\to0,$ kada $(x,y)\to(0,0),$ dok je $\theta$ proizvoljan ugao, takav da je $\theta\in(0,2\pi].$ Nakon uvođenja smene, u polazni limes dobijamo $$ \lim\limits_{(x,y)\to(0,0)}\dfrac{xy}{x^2+y^2}=\lim\limits_{\rho\to0}\dfrac{\rho^2\cos\theta\sin\theta}{\rho^2}=\cos\theta\sin\theta, $$ gde je $\theta\in(0,2\pi].$ Očigledno je da ćemo za različite vrednosti ugla $\theta$ dobijati određene vrednosti iz intervala $[-1,1].$ To znaći da granična vrednost posmatrane funkcije u tački $ ( 0 , 0 ) $ ne postoji, jer kada prilazimo tački $ ( 0 , 0 ) $ iz različitih pravaca (tj. za različite vrednosti ugla $\theta$) dobijamo razne vrednosti iz intervala $ [ - 1 , 1 ] . $

b) Možemo pisati $\dfrac{ \sin ( x y ) }{ y } = \dfrac{ \sin ( x y ) }{ x y } \cdot x . $ Važi da je $$ \lim\limits_{(x,y)\to(2,0)}\frac{\sin (xy)}{xy}=\lim\limits_{t\to 0}\frac{\sin t}{t}=1, $$ gde smo uveli smenu $ x \cdot y = t ,$ pri čemu $ t \to 0,$ kada $ ( x , y ) \to ( 2 , 0 ) . $

Tada imamo $$ \underset{ \left( x , y \right) \rightarrow \left( 2 , 0 \right) }{ \lim }\dfrac{\sin (xy)}{y}=\lim\limits_{(x,y)\to(2,0)}\frac{\sin (xy)}{xy}\cdot x=\lim\limits_{t\to 0}\frac{\sin t}{t}\cdot\lim\limits_{x\to 2}x=2. $$ c) Za $x\not=0$ i $y\not=0$ imamo da je \begin{align*} 0 & < \left|\dfrac{x^{3}+y^{3}}{x^{4}+y^{4}}\right| = \dfrac{\left|x^{3}+y^{3}\right|}{x^{4}+y^{4}} \leq\dfrac{\left|x^{3}\right|+\left|y^{3}\right|}{x^{4}+y^{4}} = \\ & = \dfrac{\left|x^{3}\right|}{x^{4}+y^{4}}+\dfrac{\left|y^{3}\right|}{x^{4}+y^{4}}\leq\\ &\leq\dfrac{\left|x^{3}\right|}{x^{4}}+\dfrac{\left|y^{3}\right|}{y^{4}}=\frac{1}{|x|}+\frac{1}{|y|}\to0, \text{ za }x\to+\infty,y\to+\infty. \end{align*} Tada je $$ \underset{\left( x,y\right) \rightarrow \left( +\infty,+\infty\right) }{\lim }\dfrac{ x^{3}+y^{3}}{x^{4}+y^{4}}=0. $$

Zadatak 5 (5 minuta)

Primer neprekidne funkcije u tački $(0,0).$

Ispitati neprekidnost date funkcije $f$ u tački $(0, 0)$

$f (x, y) = \{\begin{matrix} \frac{x^{2} - y^{2}}{\sqrt{x^{2} + y^{2}}}, & (x, y) \neq (0, 0) \\ 0, & (x, y) = (0, 0) \end{matrix}$

Rešenje: Za $(x, y) \neq (0, 0)$ je

$|f (x, y)| \leq \frac{x^{2} + y^{2}}{\sqrt{x^{2} + y^{2}}} = \sqrt{x^{2} + y^{2}} = g (x, y) \to 0$

kad $(x, y) \to (0, 0) .$ Prema tome, $f (x, y) \to 0$ kada $(x, y) \to (0, 0) .$

Kako je $f (0, 0) = 0$ funkcija je neprekidna u tački $(0, 0) .$

Zadatak 6 (5 minuta)

Ispitivanje neprekidnost funkcije u tački $(0,0).$

Ispitati neprekidnost date funkcije $f$ u tački $(0, 0)$

$f (x, y) = \{\begin{matrix} \frac{{y x}^{2} - {x y}^{4}}{x^{2} + y^{4}}, & (x, y) \neq (0, 0) \\ 0, & (x, y) = (0, 0) \end{matrix}$

Rešenje:

Za $(x, y) \neq (0, 0)$ je

$|f (x, y)| = |\frac{{y x}^{2}}{x^{2} + y^{4}} - \frac{{x y}^{4}}{x^{2} + y^{4}}| \leq \frac{|{y x}^{2}|}{x^{2} + y^{4}} + \frac{|{x y}^{4}|}{x^{2} + y^{4}} \leq \frac{|{y x}^{2}|}{x^{2}} + \frac{|{x y}^{4}|}{y^{4}} = |y| + |x| \to 0$

kada $(x, y) \to (0, 0) .$

Prema tome, $f (x, y) \to 0$ kada $(x, y) \to (0, 0) .$

Kako je $f (0, 0) = 0$ funkcija je neprekidna u tački $(0, 0) .$

Zadatak 7 (5 minuta)

Ispitivanje neprekidnost funkcije - primena Leme o dva policajca.

Ispitati neprekidnost date funkcije $f$ u tački $(0, 0)$

$f (x, y) = \{\begin{matrix} \frac{x^{3} - {3 y x}^{2}}{\sqrt{x^{2} + y^{4}}} \sin \frac{1}{x^{2} + y^{4}}, & (x, y) \neq (0, 0) \\ 0, & (x, y) = (0, 0) \end{matrix}$

Rešenje:

Za $(x, y) \neq (0, 0)$ je

$|f (x, y)| \leq \frac{x^{2} |x - 3 y|}{\sqrt{x^{2} + y^{4}}} \leq \frac{x^{2} + y^{4}}{\sqrt{x^{2} + y^{4}}} |x - 3 y| = \sqrt{x^{2} + y^{4}} |x - 3 y| = g (x, y) \to 0$

kad $(x, y) \to (0, 0) .$

Prema tome, $f (x, y) \to 0$ kada $(x, y) \to (0, 0) .$

Kako je $f (0, 0) = 0$ funkcija je neprekidna u tački $(0, 0) .$

Napomena: U ovom zadatku je korišćena nejednakost $|\sin \frac{1}{x^{2} + y^{4}}| \leq 1 .$

Zadatak 8 (10 minuta)

Određivanje prvih parcijalnih izvoda stepenih, eksponecijalnih i racionanih funkcija.

Odrediti prve parcijalne izvode za sledeće funkcije: $1) z = e^{x^{2} + y^{2} - 5 x y + 3 x}; 2) z = \frac{x + y}{x - y}; 3) z = x^{y} .$

Rešenje:

$1) z_{x}^{ˊ} = {(e^{x^{2} + y^{2} - 5 x y + 3 x})}_{x}^{ˊ} = e^{x^{2} + y^{2} - 5 x y + 3 x} ∙ {(x^{2} + y^{2} - 5 x y + 3 x)}_{x}^{ˊ} = e^{x^{2} + y^{2} - 5 x y + 3 x} ∙ (2 x - 5 y + 3)$

$z_{y}^{ˊ} = {(e^{x^{2} + y^{2} - 5 x y + 3 x})}_{y}^{ˊ} = e^{x^{2} + y^{2} - 5 x y + 3 x} ∙ {(x^{2} + y^{2} - 5 x y + 3 x)}_{y}^{ˊ} = e^{x^{2} + y^{2} - 5 x y + 3 x} ∙ (2 y - 5 x)$

$2) z_{x}^{ˊ} = {(\frac{x + y}{x - y})}_{x}^{ˊ} = \frac{{(x + y)}_{x}^{ˊ} (x - y) - (x + y) {(x - y)}_{x}^{ˊ}}{{(x - y)}^{2}} = \frac{x - y - x - y}{{(x - y)}^{2}} = \frac{- 2 y}{{(x - y)}^{2}}$

$z_{y}^{ˊ} = {(\frac{x + y}{x - y})}_{y}^{ˊ} = \frac{{(x + y)}_{y}^{ˊ} (x - y) - (x + y) {(x - y)}_{y}^{ˊ}}{{(x - y)}^{2}} = \frac{x - y + x + y}{{(x - y)}^{2}} = \frac{2 x}{{(x - y)}^{2}}$

$3) z_{x}^{ˊ} = {(x^{y})}_{x}^{ˊ} = y ∙ x^{y - 1}$

$z_{y}^{ˊ} = {(x^{y})}_{y}^{ˊ} = x^{y} ∙ \ln x$

Zadatak 9 (10 minuta)

Određivanje prvih parcijalnih izvoda logaritaskih, trigonometrijskih i skponencijalnih funkcija.

Odrediti prve parcijalne izvode za sledeće funkcije: $1) z = \ln (x + \sqrt{x^{2} + y^{2}}); 2) z = x \sin y + x e^{\frac{y}{x}} .$

$1) z_{x}^{'} = {(\ln (x + \sqrt{x^{2} + y^{2}}))}_{x}^{'} = \frac{1 + \frac{2 x}{2 \sqrt{x^{2} + y^{2}}}}{x + \sqrt{x^{2} + y^{2}}} = \frac{\frac{\sqrt{x^{2} + y^{2}} + x}{\sqrt{x^{2} + y^{2}}}}{x + \sqrt{x^{2} + y^{2}}} = \frac{1}{\sqrt{x^{2} + y^{2}}}$

$z_{y}^{'} = {(\ln (x + \sqrt{x^{2} + y^{2}}))}_{y}^{'} = \frac{\frac{2 y}{2 \sqrt{x^{2} + y^{2}}}}{x + \sqrt{x^{2} + y^{2}}} = \frac{y}{(x + \sqrt{x^{2} + y^{2}}) \sqrt{x^{2} + y^{2}}}$

$2) z_{x}^{'} = {(x \sin y + x e^{\frac{y}{x}})}_{x}^{'} = \sin y + e^{\frac{y}{x}} + x e^{\frac{y}{x}} ∙ \frac{y}{- x^{2}} = \sin y + e^{\frac{y}{x}} - \frac{y}{x} e^{\frac{y}{x}}$

$z_{y}^{'} = {(x \sin y + x e^{\frac{y}{x}})}_{y}^{'} = x \cos y + x e^{\frac{y}{x}} ∙ \frac{y}{x} = x \cos y + e^{\frac{y}{x}}$

Zadatak 10 (5 minuta)

Određivanje drugih parcijalnih izvoda

Odrediti druge parcijalne izvode funkcija: $z = e^{x y^{2}} - x^{2} y^{3}$ .

Rešenje: Prvi parcijalni izvodi su:

$\begin{matrix} z_{x}^{'} = {(e^{x y^{2}} - x^{2} y^{3})}_{x}^{'} = y^{2} e^{x y^{2}} - 2 x y^{3}, \\ z_{y}^{'} = {(e^{x y^{2}} - x^{2} y^{3})}_{y}^{'} = 2 x y e^{x y^{2}} - 3 x^{2} y^{2} . \end{matrix}$

Drugi parcijalni izvodi su:

$\begin{matrix} \begin{matrix} z_{x x}^{''} = {(z_{x}^{'})}_{x}^{'} = {(y^{2} e^{x y^{2}} - 2 x y^{3})}_{x}^{'} = y^{4} e^{x y^{2}} - 2 y^{3} \\ z_{x y}^{''} = z_{y x}^{''} = {(z_{x}^{'})}_{y}^{'} = {(y^{2} e^{x y^{2}} - 2 x y^{3})}_{y}^{'} = 2 y e^{x y^{2}} + 2 x y^{3} e^{x y^{2}} - 6 x y^{2} \end{matrix} \\ z_{y y}^{''} = {(z_{y}^{'})}_{y}^{'} = {(2 x y e^{x y^{2}} - 3 x^{2} y^{2})}_{y}^{'} = 2 x e^{x y^{2}} + 4 x^{2} y^{2} e^{x y^{2}} - 6 x^{2} y \end{matrix}$

Zadatak 11 (10 minuta)

Određivanje lokalnih ekstremnih vrednosti funkcije.

Naći lokalne ekstreme funkcije: $f (x, y) = x^{2} + x y + y^{2} - 3 x - 6 y .$

Rešenje: Nađemo prve parcijalne izvode:

$\begin{matrix} f_{x}^{ˊ} = {(x^{2} + x y + y^{2} - 3 x - 6 y)}_{x}^{ˊ} = 2 x + y - 3 \\ f_{y}^{ˊ} = {(x^{2} + x y + y^{2} - 3 x - 6 y)}_{y}^{ˊ} = x + 2 y - 6 \end{matrix}$

Rešimo sistem $f_{x}^{ˊ} = 0, f_{y}^{ˊ} = 0$

$\begin{matrix} 2 x + y - 3 = 0 \\ x + 2 y - 6 = 0 \end{matrix}$

Rešenje sistema je $x = 0, y = 3$ i to je stacionarna tačka funkcije. Da bismo ispitali da li je stacionarna tačka minimuna ili maksimuma (ili ni jedno ni drugo) potrebni su nam drugi parcijalni izvodi:

$f_{x x}^{ˊ ˊ} = {(f_{x}^{ˊ})}_{x}^{ˊ} = {(2 x + y - 3)}_{x}^{ˊ} = 2$

$f_{x y}^{ˊ ˊ} = f_{y x}^{ˊ ˊ} = {(f_{x}^{ˊ})}_{y}^{ˊ} = {(2 x + y - 3)}_{y}^{ˊ} = 1$

$f_{y y}^{ˊ ˊ} = {(f_{y}^{ˊ})}_{y}^{ˊ} = {(x + 2 y - 6)}_{y}^{ˊ} = 2$

$A = f_{x x}^{ˊ ˊ} (0, 3) = 2, B = f_{x y}^{ˊ ˊ} (0, 3) = f_{y x}^{ˊ ˊ} (0, 3) = 1, C = f_{y y}^{ˊ ˊ} (0, 3) = 2,$

$𝛾 = A C - B^{2} = 4 - 1 = 3 > 0 i A > 0 .$

Na osnovu Silvesterovog kriterijuma dobijamo da funkcija ima lokalni minimum u tački (0,3).

$f_{m i n} = f (0, 3) = 0^{2} + 0 ∙ 3 + 3^{2} - 3 ∙ 0 - 6 ∙ 3 = - 9 .$

Video klip

Snimak sa Youttube-a: lokalne ekstremen vrednosti

Zadatak 12 – 1. deo (20 minuta)

Određivanje lokalnih ekstremnih vrednosti funkcije – rešavanje sistema, određivanje stacionarne tačke i drugih parcijalnih izvoda.

Naći lokalne ekstreme funkcija: $f (x, y) = e^{x - y} (x^{2} - 2 y^{2}) .$

Rešenje. Nađemo prve parcijalne izvode:

$f_{x}^{ˊ} = {(e^{x - y} (x^{2} - 2 y^{2}))}_{x}^{ˊ} = e^{x - y} (x^{2} - 2 y^{2}) + e^{x - y} ∙ 2 x = e^{x - y} (x^{2} - 2 y^{2} + 2 x)$

$f_{y}^{ˊ} = {(e^{x - y} (x^{2} - 2 y^{2}))}_{y}^{ˊ} = - e^{x - y} (x^{2} - 2 y^{2}) + e^{x - y} ∙ (- 4 y) = e^{x - y} (- x^{2} + 2 y^{2} - 4 y)$

Dobijamo sistem:

$\begin{matrix} \begin{matrix} \begin{matrix} \begin{matrix} \begin{matrix} x^{2} - 2 y^{2} + 2 x = 0 \\ \underline{- x^{2} + 2 y^{2} - 4 y = 0} \end{matrix}\} & + \end{matrix} \\ \begin{matrix} x^{2} - 2 y^{2} + 2 x = 0 \\ \underline{2 x - 4 y = 0} \end{matrix} \end{matrix} \\ \begin{matrix} x^{2} - 2 y^{2} + 2 x = 0 \\ \underline{x = 2 y} \end{matrix} \end{matrix} \\ \begin{matrix} \begin{matrix} 4 y^{2} - 2 y^{2} + 4 y = 0 \\ \underline{x = 2 y} \end{matrix} \\ \begin{matrix} 2 y (y + 2) = 0 \\ \underline{x = 2 y} \end{matrix} \end{matrix} \end{matrix}$

Rešenja sistema su: $x = 0, y = 0$ i $x = - 4, y = - 2$ . Dakle, tačke $М (0, 0)$ и $N (- 4, - 2)$ su stacionarne tačke funkcije.

Drugi parcijalni izvodi

$f_{x x}^{ˊ ˊ} = {(f_{x}^{ˊ})}_{x}^{ˊ} = {(e^{x - y} (x^{2} - 2 y^{2} + 2 x))}_{x}^{ˊ} = e^{x - y} (x^{2} - 2 y^{2} + 2 x) + e^{x - y} (2 x + 2) = e^{x - y} (x^{2} - 2 y^{2} + 4 x + 2)$

$f_{x y}^{ˊ ˊ} = f_{y x}^{ˊ ˊ} = {(f_{x}^{ˊ})}_{y}^{ˊ} = {(e^{x - y} (x^{2} - 2 y^{2} + 2 x))}_{y}^{ˊ} = - e^{x - y} (x^{2} - 2 y^{2} + 2 x) + e^{x - y} (- 4 y) = - e^{x - y} (x^{2} - 2 y^{2} + 2 x + 4 y)$

$f_{y y}^{ˊ ˊ} = {(f_{y}^{ˊ})}_{y}^{ˊ} = {(e^{x - y} (- x^{2} + 2 y^{2} - 4 y))}_{y}^{ˊ} = - e^{x - y} (- x^{2} + 2 y^{2} - 4 y) + e^{x - y} (4 y - 4) = e^{x - y} (x^{2} - 2 y^{2} + 8 y - 4)$

Zadatak 12 – 2. deo

Određivanje lokalnih ekstremnih vrednosti funkcije – primena Silvesterovog kriterijuma

Odredimo vrednosti drugih parcijalnih izvoda u tački $М$ .

$A = f_{x x}^{ˊ ˊ} (0, 0) = e^{0 - 0} (0^{2} - 2 ∙ 0^{2} + 4 ∙ 0 + 2) = 2, B = f_{x y}^{ˊ ˊ} (0, 0) = f_{y x}^{ˊ ˊ} (0, 0) = 0, C = f_{y y}^{ˊ ˊ} (0, 0) = - 4 .$

$𝛾 = A C - B^{2} = |\begin{matrix} 2 & 0 \\ 0 & - 4 \end{matrix}| = - 8 < 0 .$

Zaključujemo da tačka $М (0, 0)$ nije tačka ekstremuma.

Odredimo vrednosti drugih parcijalnih izvoda u tački $N$ .

$A = f_{x x}^{ˊ ˊ} (- 4, - 2) = e^{- 4 + 2} ({(- 4)}^{2} - 2 ∙ {(- 2)}^{2} + 4 ∙ (- 4) + 2) = - 6 e^{- 2}$

$B = f_{x y}^{ˊ ˊ} (- 4, - 2) = f_{y x}^{ˊ ˊ} (- 4, - 2) = - e^{- 4 + 2} ({(- 4)}^{2} - 2 ∙ {(- 2)}^{2} + 2 ∙ (- 4) + 4 ∙ (- 2)) = 8 e^{- 2}$

$C = f_{y y}^{ˊ ˊ} (- 4, - 2) = e^{- 4 + 2} ({(- 4)}^{2} - 2 ∙ {(- 2)}^{2} + 8 ∙ (- 2) - 4) = - 12 e^{- 2}$

$𝛾 = A C - B^{2} = (72 - 64) e^{- 2} = 8 e^{- 2} > 0 .$

Kako je

$A = f_{x x}^{ˊ ˊ} (- 4, - 2) = - 6 e^{- 2} < 0,$

zaključujemo da je tačka $N (- 4, - 2)$ tačka lokalnog maksimuma koji iznosi

$f_{m a x} = f (- 4, - 2) = e^{- 4 + 2} ({(- 4)}^{2} - 2 ∙ {(- 2)}^{2}) = 8 e^{- 2} .$

Zadatak 13 – 1. deo (20 minuta)

Određivanje lokalnih ekstremnih vrednosti funkcije – rešavanje sistema, određivanje stacionarne tačke i određivanje drugih parcijalnih izvoda.

Odredi lokalne ekstremume zadate funkcije $f (x, y) = e^{- x^{2} - y^{2}} (x^{2} + 2 y^{2})$ .

Rešenje: Određivanje stacionarnih tačaka

$\underline{\begin{matrix} f_{x}^{ˊ} = 0 \\ f_{y}^{ˊ} = 0 \end{matrix}}$

$f_{x}^{ˊ} = e^{- x^{2} - y^{2}} (- 2 x) (x^{2} + 2 y^{2}) + e^{- x^{2} - y^{2}} (x^{2} + 2 y^{2}) (2 x) = e^{- x^{2} - y^{2}} ∙ 2 x ∙ (1 - x^{2} - 2 y^{2}) = 0$

$f_{y}^{ˊ} = e^{- x^{2} - y^{2}} (- 2 y) (x^{2} + 2 y^{2}) + e^{- x^{2} - y^{2}} (x^{2} + 2 y^{2}) (4 y) = e^{- x^{2} - y^{2}} ∙ 2 y ∙ (2 - x^{2} - 2 y^{2}) = 0$

$\underline{\begin{matrix} \begin{matrix} 2 x ∙ (1 - x^{2} - 2 y^{2}) = 0 \end{matrix} & (1) \\ 2 y ∙ (2 - x^{2} - 2 y^{2}) = 0 & (2) \end{matrix}}$

$(1) \Rightarrow \begin{matrix} x = 0 & ⋁ & 1 - x^{2} - 2 y^{2} = 0 \end{matrix}$

$(2) \Rightarrow \begin{matrix} y = 0 & ⋁ & 2 - x^{2} - 2 y^{2} = 0 \end{matrix}$

$\begin{matrix} \begin{matrix} I s l u č a j & I I s l u č a j & I I I s l u č a j & I V s l u č a j \\ x = 0 & x = 0 & y = 0 & x^{2} + 2 y^{2} = 2 \\ y = 0 & x^{2} + 2 y^{2} = 2 & x^{2} + 2 y^{2} = 1 & x^{2} + 2 y^{2} = 1 \\ S_{1} (0, 0) & y = \pm 1 & x = \pm 1 & n e m a r e š e n j a \\ S_{2} (0, - 1) & S_{4} (- 1, 0) \\ S_{3} (0, 1) & S_{5} (1, 0) \end{matrix} \end{matrix}$

Odredimo druge parcijalne izvode

$f_{x x}^{ˊ ˊ} = e^{- x^{2} - y^{2}} ∙ 2 x ∙ (1 - x^{2} - 2 y^{2}) ∙ (2 x) + e^{- x^{2} - y^{2}} ∙ 2 ∙ (1 - x^{2} - 2 y^{2}) + e^{- x^{2} - y^{2}} ∙ 2 x ∙ (- 2 x)$

$f_{x y}^{ˊ ˊ} = e^{- x^{2} - y^{2}} ∙ 2 x ∙ (1 - x^{2} - 2 y^{2}) ∙ (- 2 y) + e^{- x^{2} - y^{2}} ∙ 2 x ∙ (- 4 y)$

$f_{y y}^{ˊ ˊ} = e^{- x^{2} - y^{2}} ∙ 2 y ∙ (2 - x^{2} - 2 y^{2}) ∙ (- 2 y) + e^{- x^{2} - y^{2}} ∙ 2 ∙ (2 - x^{2} - 2 y^{2}) + e^{- x^{2} - y^{2}} ∙ 2 y (- 4 y)$

Zadatak 13 – 2. deo

Određivanje lokalnih ekstremnih vrednosti funkcije – primena Silvesterovog kriterijuma.

Primenjujemo Silvesterov kriterijum:

Tačka $𝑺_{𝟏} (𝟎, 𝟎)$

$\begin{matrix} A = 2, B = 0, C = 4 \\ 𝛾 = 8 > 0 . \end{matrix}$

Kako je

$A = f_{x x}^{ˊ ˊ} (0, 0) = 2 > 0 .$

Tačka $S_{1} (0, 0)$ je tačka lokalnog minimuma i $f_{m i n} (0, 0) = 0$ .

Tačka $𝑺_{𝟐} (𝟎, - 𝟏)$

$A = - 2 \frac{1}{e}, B = 0, C = - 8 \frac{1}{e},$

$𝛾 = \frac{16}{e^{2}} > 0 .$

Kako je

$A = f_{x x}^{ˊ ˊ} (0, - 1) = - 2 \frac{1}{e} < 0 .$

Tačka $S_{2} (0, - 1)$ je tačka lokalnog maksimuma i $f_{m a x} (0, - 1) = 2 e^{- 1}$ .

Tačka $𝑺_{𝟑} (𝟎, 𝟏)$

$A = - 2 \frac{1}{e}, B = 0, C = - 8 \frac{1}{e},$

$𝛾 = \frac{16}{e^{2}} > 0 .$

Kako je

$A = f_{x x}^{ˊ ˊ} (0, - 1) = - 2 \frac{1}{e} < 0 .$

Tačka $S_{3} (0, 1)$ je tačka lokalnog maksimuma i $f_{m a x} (0, 1) = 2 e^{- 1}$ .

Tačka $𝑺_{𝟒} (- 𝟏, 𝟎)$

$A = - 4 \frac{1}{e}, B = 0, C = 2 \frac{1}{e},$

$𝛾 = \frac{- 8}{e^{2}} < 0 .$

Tačka $S_{4} (- 1, 0)$ nije tačka lokalnog ekstremuma.

Tačka $𝑺_{𝟓} (𝟏, 𝟎)$

$A = - 4 \frac{1}{e}, B = 0, C = 2 \frac{1}{e},$

$𝛾 = \frac{- 8}{e^{2}} < 0 .$

Tačka $S_{5} (1, 0)$ nije tačka lokalnog ekstremuma.