- Pojam i podela hi-kvadrat testova
- Hi-kvadrat test za ispitivanje kvaliteta podudaranja
- Prvi primer - poslednja tri koraka
- Sprovođenje hi-kvadrat test za ispitivanje kvaliteta podudaranja u SPSS-u
- Postupak za obavljanje hi-kvadrat testa kvaliteta podudaranja u SPSS-u
- Tumačenje i predstavljanje rezultata hi-kvadrat testa podudaranja u SPSS-u
- Hi-kvadrat test nezavisnosti
- Koraci kod testa nezavisnosti
- Prvi primer testa nezavisnosti
- Sprovođenje testa nezavisnosti za prvi primer
- Drugi primer testa nezavisnosti
- Sprovođenje testa nezavisnosti za drugi primer
- Sprovođenje hi-kvadrat test nezavisnosti u SPSS-u
- Postupak za obavljanje hi-kvadrat testa nezavisnosti u SPSS-u
- Rezultati postupka za obavljanje hi-kvadrat testa nezavisnosti u SPSS-u
- Tumačenje rezultata hi-kvadrat testa nezavisnosti u SPSS-u
- Tabela kontigencije kao deo izlaznih rezultata
- Izračunavanje veličine uticaja
- Hi-kvadrat test nezavisnosti - video
Pokazali smo kako vršimo ocenjivanje i testiranje hipoteza o proporciji (relativnoj frekvenciji) u skupu jednog od samo dva moguća modaliteta. Na primer, učešće stranih turista u ukupnom broju turista, učešće KV radnika u ukupnom broju zaposlenih, učešće studenata Ekonomskog fakulteta u ukupnom broju studenata univerziteta itd. Istraživanje proporcije jednog od dva moguća modaliteta je specijalan slučaj analize proporcije (relativnog učešća) više modaliteta.
Analizu relativne frekvencije više modaliteta vršimo $\bf \chi^{2}$ $\bf testom$. Osnovu ovog oblika testiranja čini upoređenje empirijskih i očekivanih (teorijskih) frekvencija, pri čemu empirijske frekvencije dobijamo prikupljanjem podataka, a očekivane izračunavamo u zavisnosti od pretpostavljenog rasporeda osnovnog skupa. Meru odstupanja empirijskih od očekivanih frekvencija označavamo sa $\chi^{2}$ i izračunavamo pomoću statistike testa: $$\chi^{2}=\sum_{i=1}^r\frac{(f_i-f_i')^2}{f_i'}$$ gde su $f_i$ - empirijske frekvencije; $f_i'$ - očekivane frekvencije, a $r$ - broj modaliteta posmatranog obeležja (intervalnih grupa ili atributivnih grupa).
$\textbf {Napomena:}$ Prag testa, ako se vrši pridruživanje, se određuje tek nakon pridruživanja, gde se smanjuje broj frekvencija.
Testovi zasnovani na hi-kvadrat rasporedu obuhvataju čitav niz problema koji se mogu odnositi na modalitete jednog ili više obeležja. Naime, oni služe za:
2) ispitivanje homogenosti skupa i
3) ispitivanje nezavisnosti dva obeležja.
U ovoj lekciji akcenat će biti na druga dva ispitivanja. Naime, objasniće se test homogenosti i test nezavisnosti, tj. kako se svaki od ovih testova sprovodi ručno, a kako uz pomoć SPSS-a.
Primenom hi-kvadrat testa možemo dobiti odgovor na pitanje da li su proporcije nekih osnovnih skupova značajno različite. Test jednakosti (razlike) za više proporcija nazivamo testom homogenosti ili testom za ispitivanje kvaliteta podudaranja. Postupak testiranja se sprovodi na sledeći način:
2) Izbor statistike testa;
3) Određivanje kritične vrednosti (praga) testa: $\chi_{\nu; \alpha}^{2}$, pri čemu je $\nu=r-1$, a $r$ predstavlja broj redova;
4) Definisanje pravila odlučivanja:
- $H_0$ prihvatamo za $\chi^{2} < \chi_{\nu; \alpha}^{2}$ i
- $H_0$ ne prihvatamo za $\chi^{2} \geq \chi_{\nu; \alpha}^{2}$
5) Određivanje vrednosti $\chi^{2}$ testa i
6) Donošenje odluke.
$\textbf {Primer 1.}$ Ispitivali smo mišljenje roditelja o uvođenju novog nastavnog programa u 5 osnovnih škola u Kragujevcu. Postavili smo im pitanje: Da li su za novi nastavni program? Dobijene odgovore dali smo u narednoj tabeli:
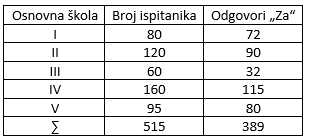
Slika-1 Rezultati ispitivanja mišljenja roditelja o uvođenju novog nastavnog programa u 5 osnovnih škola [Izvor: sopstvena izrada]
Pre nego što se počne sa testiranjem, neophodno je da se izračunaju relativne frekvencije (učešća) po školama: $$p_1=\frac{72}{80}=0,90; p_2=\frac{90}{120}=0,75; p_3=\frac{32}{60}=0,533; p_4=\frac{115}{160}=0,719; \\ p_5=\frac{80}{95}=0,842 \Rightarrow p_s=\frac{\sum f_i}{\sum n_i}=\frac{389}{515}=0,755$$ 1) $H_0: \pi_1=\pi_2=\pi_3=\pi_4=\pi_5=0,755$ i $H_1:$ obrnuto.
2) izbor statistike testa: $\chi^{2}$ test
3) prag testa: $\chi_{\nu;\alpha}^{2}=?, \alpha=0,05, \nu=r-1=5-1=4 \Rightarrow \chi_{4;0,05}^{2}=9,488$ (vrednost se čita iz Tabice 3.)
- $H_0$ prihvatamo za $\chi^{2} < \chi_{\nu; \alpha}^{2}$ i
- $H_0$ ne prihvatamo za $\chi^{2} \geq \chi_{\nu; \alpha}^{2}$
5) Određivanje vrednosti $\chi^{2}$ testa: $f_i'=?, f_i'=n_i\cdot p_s$
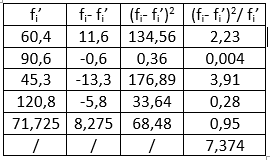
Slika-2 Kalkulacija vrednosti hi-kvadrat [Izvor: sopstvena izrada]
6) Donošenje odluke: $\chi_{\nu;\alpha}^{2}=9,488$ i $\chi^{2}=7,374 \Rightarrow \chi^{2} < \chi_{\nu;\alpha}^{2} \Rightarrow$ prihvata se $H_0$, tj. proporcije u svim osnovnim skupovima (osnovnim školama) su jednake. Prema tome, stavovi roditelja u ovih 5 škola, u vezi sa uvođenjem novog nastavnog programa, međusobno se ne razlikuju (razlike su slučajne).
Ovaj test, koji se naziva i hi-kvadrat test jednog uzorka, često se upotrebljava za poređenje proporcije slučajeva iz određenog uzorka s hipotetičkim vrednostima ili onima prethodno dobijenim u nekoj poredbenoj populaciji. Dovoljno je da datoteka s podacima sadrži samo jednu kategorijsku promenljivu i određenu proporciju s kojom želite da uporedite dobijene rezultate. Može se ispitati hipoteza da nema razlike u proporciji kategorija (50%/50%) ili određena proporcija dobijena u nekoj prethodnoj studiji.
Primer istraživačkog pitanja: Istražiće se da li je procentualni udeo pušača u populaciji opisanoj u datoteci survey3ED.sav ekvivalentan onome (20%) navedenom u literaturi prethodno objavljene velike austrijske studije.
Šta vam treba:
- jedna kategorijska promenljiva sa dve ili više kategorija: pušač (Da/Ne) i
- hipotetička proporcija (20% pušača; 80% nepušača ili 0,2/0,8).
Da biste pratili ovaj primer, otvorite datoteku survey4ED.sav.
- Otvorite meni Analyze, pritisnite njegovu stavku No-parametric tests, pa Legacy Dialogs i zatim Chi-Square;
- Pritisnite kategorijsku promenljivu smoke (tj. pušač), pa pritisnite strelicu da biste promenljivu prebacili u polje Test Variable List;
- U odeljku Expected Values pritisnite opciju Values. U polje Values treba da upišete dva broja. Prvi broj (0,2) odgovara očekivanoj proporciji prve šifrovane vrednosti te promenljive (1 = da, pušač). Pritisnite dugme Add. Upišite drugi broj (0,8), što je očekivana proporcija druge šifrovane vrednosti te promenljive (2 = ne, nepušač). Pritisnite dugme Add. Ukoliko promenljiva ima više od dve moguće vrednosti, za svaku od njih treba upisati odgovarajuću proporciju;
- Pritisnite OK.
Evo i kako izgledaju rezultati tog postupka:
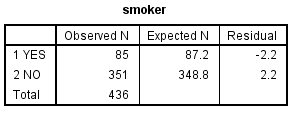
Slika-3 smoker [Izvor: sopstvena izrada]

Slika-4 Test Statistics [Izvor: sopstvena izrada]
Tumačenje rezultata
U prvoj tabeli date su opažane učestalosti (frekvencije) iz tekuće datoteke s podacima; vidimo da su pušači njih 85 od ukupno 436 (19,5%). U koloni Expected N date su učestalosti očekivane na osnovu prethodno zadate proporcije (20%). U ovom slučaju, očekivano je da bude 87 pušača, a opažano je 85.
U tabeli Test Statistics dati su rezultati SPSS-ovog testa Chi-Square, koji poredi očekivane i opažane vrednosti. U ovom slučaju, razlika između njih je vrlo mala, a nije ni statistički značajna (Sig. = 0,79; p > 0,05).
Predstavljanje rezultata
Treba navesti vrednost hi-kvadrat, broj stepeni slobode (engl. degrees od freedom, df) i vrednost p (prikazana kao Asymp. Sig.).
Hi kvadrat test podudaranja pokazuje da se proporcija pušača u tekućem uzorku (19,5%), ne razlikuje mnogo od vrednosti 20% dobijenoj u prethodnoj austrijskoj studiji, X2 (1, n = 436) = 0,07, p < 0,79.
Hi-kvadrat analizom se pored testiranja oblika rasporeda, testira i postojanje neke veze - asocijacije između kategorijskih promenljivih. Naime, hi-kvadrat testom nezavisnosti (hi-kvadrat testom statistika) se istražuje veza između dve kategorijske promenljive. Svaka od njih može imati dve ili više kategorija. Test poredi učestalosti ili proporcije slučajeva opažane u svakoj od kategorija, s vrednostima koje bi bile očekivane da između dve merene promenljive nema nikakve veze. Tačnije, nulta hipoteza za ovaj test je da ne postoji veza između kategorijskih promenljivih, tj. da su posmatrane učestalosti (frekvencije) jednake očekivanim frekvencijama. Ovaj test se zasniva na unakrsnoj tabeli (tabeli kontigencije), tj. u tabeli u kojoj su kategorije jedne promenljive ukrštene s kategorijama druge (npr. muškarci/žene; pušač/nepušač); svaka ćelija unakrsne tabele sadrži po jednu kombinaciju kategorija posmatranih promenljivih.
Elementi za test nezavisnosti i statistika testa
Broj elementarnih jedinica koje pripadaju udruženim modalitetima $f_{ij}$, za $i=1,2,...,r$ i $j=1,2,...,k$ nazivamo $\bf kontigentom$. Kontigenti elementarnih jedinica formiraju $\textbf {tabelu kontigencije}$:
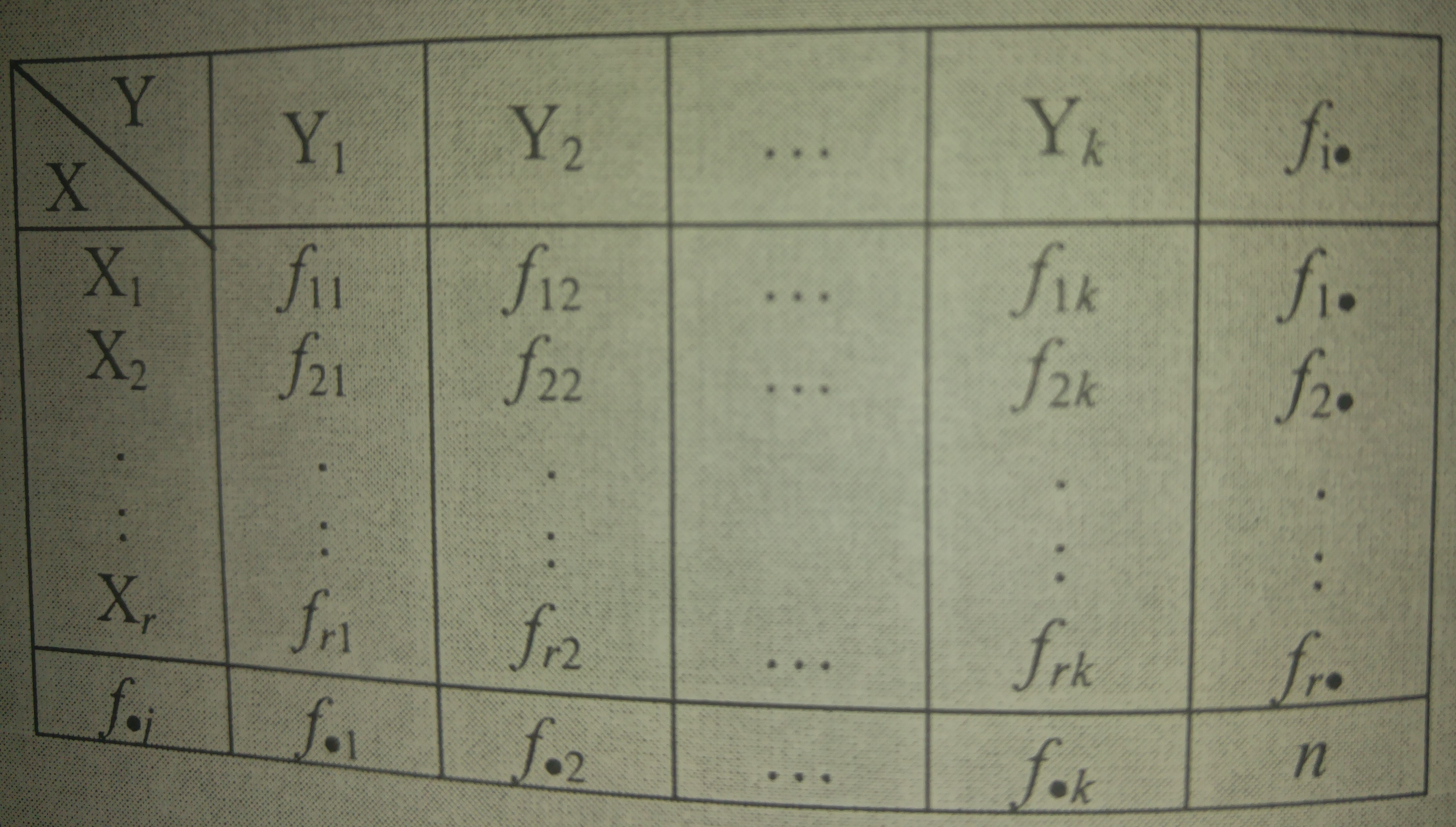
Slika-5 Tabela kontigencije [Izvor: Đorđević, 2006]
Razlika empirijskih kotigenata $f_{ij}$ i očekivanih kontigenata $f_{ij}'$ data je $\bf statistikom$ $\bf \chi^{2}$: $$\chi^{2}=\sum_{i=1}^r\sum_{j=1}^k\frac{(f_{ij}-f_{ij}')^2}{f_{ij}'},$$ koja je slučajna promenljiva i ima približno $\chi^{2}$ raspored sa $(r-1) \cdot (k-1)$ stepena slobode.
Testiramo nezavisnost dva atributivna (numerička) obeležja na osnovu slučajnog uzorka koji pripada klasi velikih uzoraka ($n\geq30$)
1) Nulta hipoteza je: $H_0$: Obeležja su nezavisna ($\textbf {uvek nezavisno!}$); Alternativna hipoteza je: $H_1$: Obeležja su zavisna;
2) Testiranje $H_0$ sprovodimo $\chi^{2}$ tetsom (jednosmerni test) sa oblašću odbacivanja $H_0$ na desnoj strani rasporeda;
3) Nivo značajnosti testa je $\alpha$. $\textbf {Kritična vrednost testa}$ je $\chi_{\nu,\alpha}^{2}$, gde je $\nu=(r-1)\cdot(k-1)$ stepena slobode (skup nema odgovarajući parametar);
4) Definisanje pravila odlučivanja:
- $H_0$ prihvatamo za $\chi^{2} < \chi_{\nu; \alpha}^{2}$ i
- $H_0$ ne prihvatamo za $\chi^{2} \geq \chi_{\nu; \alpha}^{2}$
5) Određivanje vrednosti $\chi^{2}$ testa i
6) Donošenje odluke.
Kada posmatrana obeležja $X$ i $Y$ imaju jednak broj modaliteta upotrebljavamo $\textbf {Pirsonov koeficijent kontigencije C}$ koga izračunavamo pomoću vrednosti $\chi^{2}$ po formuli: $$C=\sqrt{\frac{\chi^{2}}{n+\chi^{2}}}$$ gde je $n$ veličina uzorka, a formulu za $\chi^{2}$ smo dali u prethodnom odeljku.
Vrednost Pirsonovog koeficijenta kontigencije je pozitivna. Kreće se u intervalu od 0 do 1. Minimalna vrednost koeficijenta kontigencije je nula (ne postoji međuzavisnost posmatranih obeležja), a maksimalna zavisi od broja modaliteta posmatranog obeležja, odnosno od $r$ ili $k$, jer je $r=k$. $\textit {Maksimalna vrednost}$ koeficijenta kotigencije ($C_{max}$) služi nam za poređenje sa realizovanom vrednošću $C$.
Obrazac za $C_{max}$ je: $$C_{max}=\sqrt{\frac{r-1}{r}} \ ili \ C_{max}=\sqrt{\frac{k-1}{k}}$$ Maksimalna vrednost koeficijenta kontigencije je pokazatelj najjačeg slaganja posmatranih modaliteta. $C_{max}$ sa povećanjem broja posmatranih modaliteta obeležja teži jedinici. Uvek kada je matrica $3\times3$ (ili $4\times4$), $C_{max}$ je uvek ista za bilo koje dve vrste obeležja.
$\textbf {Primer 1.}$ Ispitujemo da li vrsta leka utiče na zdravstveno stanje bolisnika. Slučajan uzorak dao je sledeći rezultat:
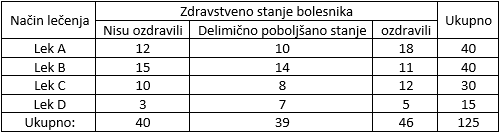
Slika-6 Raspored bolesnika prema načinu lečenja u zdravstvenom centru [Izvor: sopstvena izrada]
Pre testiranja izračunavamo očekivane kontigente po formuli: $$f_{ij}'=\frac{f_{i\star}\cdot f_{\star j}}{n}$$ Tako su, na primer: $$f_{11}'=\frac{f_{1\star}\cdot f_{\star 1}}{n}=\frac{40\cdot40}{125}=12,8; f_{12}'=\frac{f_{1\star}\cdot f_{\star 2}}{n}=\frac{39\cdot40}{125}=12,48; \ itd.$$ Empirijske i očekivane kontigente uneli smo u narednu tabelu.
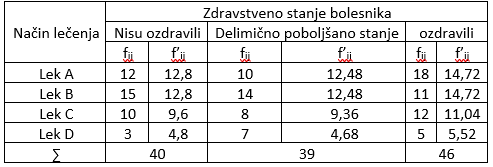
Slika-7 Empirijske i očekivane frekvencije na osnovu podataka iz prethodne tabele [Izvor: sopstvena izrada]
U tabeli se javljaju tzv. male očekivane frekvencije, $f_{ij}'<5$, pa vršimo pregrupisanje podataka i dobijamo sledeću tabelu.
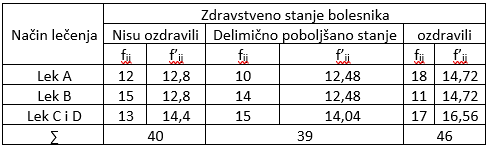
Slika-8 Empirijske i očekivane frekvencije [Izvor: sopstvena izrada]
Empirijske i očekivane kontigente unosimo u tabelu za kalkulaciju $\chi^{2}$ testa (tabela 4.):
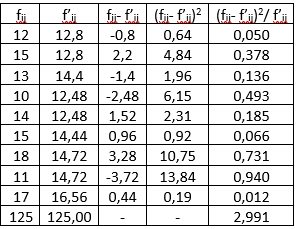
Slika-9 Kalkulacija vrednosti hi-kvadrat [Izvor: sopstvena izrada]
2) Testiranje vršimo jednosmernim $\chi^{2}$ testom (oblast odbacivanja $H_0$ je desno);
3) Nivo značajnosti testa je $\alpha=0,05$. Broj stepeni slobode je $\nu=(r-1)\cdot(k-1)=(3-1)\cdot(3-1)=4$. Određujemo na osnovu preuređene tabele kontigencije ($r=3$ i $k=3$). Kritična vrednost testa je: $\chi_{\nu;\alpha}^{2}=\chi_{4;0,05}^{2}=9,488$ (vrednost čitamo iz Tablice 3.);
- $H_0$ prihvatamo za $\chi^{2} < \chi_{\nu; \alpha}^{2}$ i
- $H_0$ ne prihvatamo za $\chi^{2} \geq \chi_{\nu; \alpha}^{2}$
5) Postupak izračunavanja vrednosti $\chi^{2}$ dali smo u Tabeli 4. Vrednost statistike testa (zbir zadnje kolone Tabele 4.) je: $$\chi^{2}=\sum_{i=1}^r\sum_{j=1}^k\frac{(f_{ij}-f_{ij}')^2}{f_{ij}'}=2,991$$ 6) Nulta hipoteza se prihvata jer je: $\chi^{2}=2,991<\chi_{4,0,05}^{2}=9,488$
Izvodimo zaključak da su posmatrana obeležja nezavisna: Zdravstveno stanje bolesnika ne zavisi od vrste leka kojim se leči uz rizik greške od 0,05.
$\textbf {Napomena:}$ Pošto smo usvojili nultu hipotezu, u daljem postupku ne bi trebalo pristupiti izračunavanju međuzavisnosti posmatranih obeležja. Međutim, ukoliko se analiza i nastavi, zaključak u pogledu međuzavisnosti posmatranih obeležja se mora podudariti sa prethodno formulisanim zaključkom. Ukoliko je usvojena $H_1$, obavezno se pristupa ispitivanju međuzavisnosti posmatranih obeležja.
$\textbf {Primer 2.}$ U jednom preduzeću pratimo broj neispravnih proizvoda u zavisnosti od radnog iskustva radnika. Snimanje škarta u proizvodnji vršeno je na uzorku. Rezultat je prikazan u narednoj tabeli (primer testiranja modaliteta numeričkih obeležja):
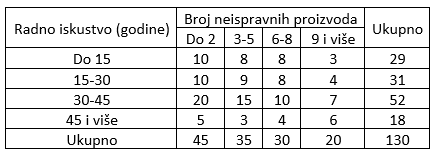
Slika-10 Tabela kontigencije: Raspored radnika prema radnom stažu i broju neispravnih proizvoda [Izvor: sopstvena izrada]
Pre testiranja izračunavamo očekivane kontigente po formuli: $$f_{ij}'=\frac{f_{i\star}\cdot f_{\star j}}{n}$$ Tako su, na primer: $$f_{11}'=\frac{f_{1\star}\cdot f_{\star 1}}{n}=\frac{45\cdot29}{130}=10,04; f_{12}'=\frac{f_{1\star}\cdot f_{\star 2}}{n}=\frac{35\cdot29}{130}=7,81; \ itd.$$
Empirijske i očekivane kontigente uneli smo u narednu tabelu.
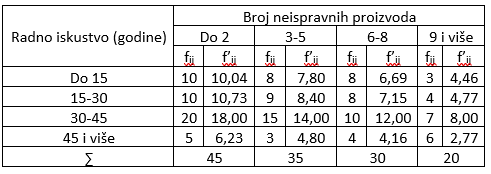
Slika-11 Empirijske i očekivane frekvencije na osnovu podataka prethodne tabele [Izvor: sopstvena izrada]
U tabeli se javljaju tzv. male očekivane frekvencije, $f_{ij}'<5$, pa vršimo pregrupisanje podataka i dobijamo sledeću tabelu.
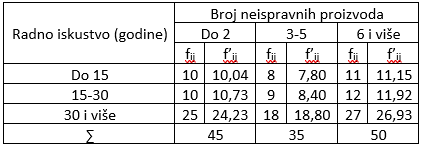
Slika-12 Empirijske i očekivane frekvencije [Izvor: sopstvena izrada]
Empirijske i očekivane kontigente unosimo u tabelu za kalkulaciju $\chi^{2}$ testa (tabela 4.):
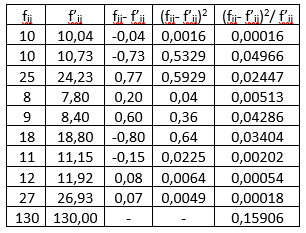
Slika-13 Kalkulacija vrednosti hi-kvadrat [Izvor: sopstvena izrada]
2) Testiranje vršimo jednosmernim $\chi^{2}$ testom (oblast odbacivanja $H_0$ je desno);
3) Nivo značajnosti testa je $\alpha=0,05$. Broj stepeni slobode je $\nu=(r-1)\cdot(k-1)=(3-1)\cdot(3-1)=4$. Određujemo na osnovu preuređene tabele kontigencije ($r=3$ i $k=3$). Kritična vrednost testa je: $\chi_{\nu;\alpha}^{2}=\chi_{4;0,05}^{2}=9,488$ (vrednost čitamo iz Tablice 3.);
4) Definisanje pravila odlučivanja:
- $H_0$ prihvatamo za $\chi^{2} < \chi_{\nu; \alpha}^{2}$ i
- $H_0$ ne prihvatamo za $\chi^{2} \geq \chi_{\nu; \alpha}^{2}$
Izvodimo zaključak da su posmatrana obeležja nezavisna: Broj neispravnih proizvoda ne zavisi od radnog iskustva uz rizik greške od 0,05.
Možemo izračunati koeficijent kontigencije koji pokazuje stepen korelacione veze između dva obeležja: $$C=\sqrt{\frac{\chi^{2}}{n+\chi^{2}}}=\sqrt{\frac{0,159}{130+0,159}}=0,0349$$ Za tabelu kontigencije $3\times3$ maksimalna vrednost je: $$C_{max}=\sqrt{\frac{k-1}{k}}=\sqrt{\frac{3-1}{3}}=0,816$$ Možemo reći da ne postoji korelaciona veza između posmatranih obeležja jer je izračunata vrednost $C=0,0349$ blizu nule. Dobijena vrednost koeficijenta kontigencije je u saglasnosti sa zaključkom $\chi^{2}$ testa da su posmatrana obeležja nezavisna.
Kada SPSS naiđe na tabelu 2 sa 2 (po dve kategorije u svakoj promenljivoj), rezultat hi-kvadrat testa obuhvata i jednu dodatnu "korekciju neprekidnosti prema Jejtsu" (engl. Yates' Correction for Continuity). Ona bi trebalo da kompenzuje (po mišljenju nekih autora) precenjenu vrednost hi-kvadrat koja se dobija u tabeli 2 sa 2.
U sledećem postupku, na primeru datoteke survey4ED.sav biće pokazano kako se upotrebljava hi-kvadrat test za projekat 2 sa 2. Kada studija obuhvata promenljive s više od dve kategorije (npr. 2 sa 3, 4 sa 4), videćete da se izlaz iz SPSS-a neznatno razlikuje.
Primer istraživačkog pitanja: Pitanje se može formulisati na više načina - postoji li veza (zavisnost) između pola i pušačkog ponašanja? Da li su muškarci češće pušači od žena? Da li je proporcija muškaraca jednaka toj proporciji kod žena?
Šta vam treba: Dve kategorijske promenljive sa po dve ili više kategorija - pol (Muškarac/Žena) i pušač (Da/Ne).
Dodatne pretpostavke: Najmanja očekivana učestalost u svim ćelijama trebalo bi da bude 5 ili više. Neki autori predlažu blaže kriterijume: najmanje 80 procenata ćelija trebalo bi da imaju očekivane učestalosti 5 ili više. Za tabelu 2 sa 2, preporučuje se da očekivana učestalost bude najmanje 10. Kada tabela 2 sa 2 ne zadovoljava ovu pretpostavku, umesto vrednosti hi-kvadrat treba upotrebiti Fišerov "tačan pokazatelj verovatnoće" (engl. Fisher's Exact Probability Test). Njega automatski generiše SPSS i navodi u sklopu rezultata hi-kvadrat testa.
Da biste pratili ovaj primer, otvorite datoteku survey4ED.sav.
- Otvorite meni Analyze, pritisnite stavku Descriptive Statistics, zatim Crosstabs;
- Pritisnite onu promenljivu (npr. sex/pol) čije će kategorije zauzimati redove tabele; pritisnite strelicu da biste izabranu promenljivu prebacili u polje Row(s);
- Pritisnite onu promenljivu (npr. smoke/pušač) čije će kategorije zauzimati kolone tabele, pa pritisnite strelicu da biste izabranu promenljivu prebacili u polje Column(s);
- Pritisnite dugme Statistics. Potvrdite polje Chi-Square i Phi and Cramer's V. Pritisnite Continue.
- Pritisnite dugme Cells. U polju Counts pritisnite Observed. U odeljku Percentage potvrdite polja Row, Column i Total i
- Pritisnite Continue i zatim OK.
Sledi deo rezultata opisanog postupka za tabelu 2 sa 2. Rezultat se malo razlikuje za promenljive s više od dve kategorije, ali u njemu i dalje treba tražiti iste ključne podatke.
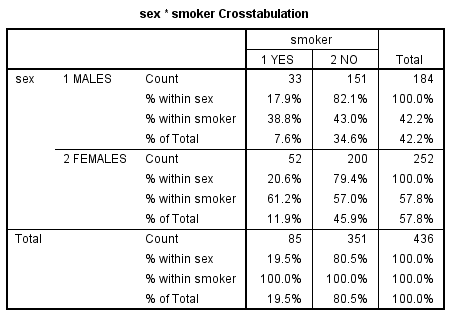
Slika-14 sex * smoker Crosstabulation [Izvor: sopstvena izrada]
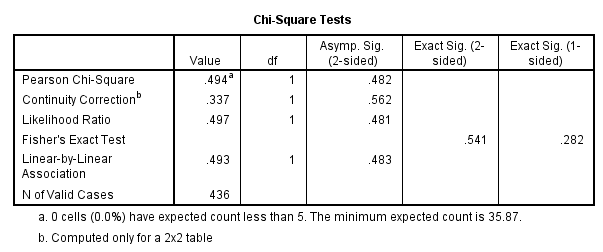
Slika-15 Chi-Square Test [Izvor: sopstvena izrada]
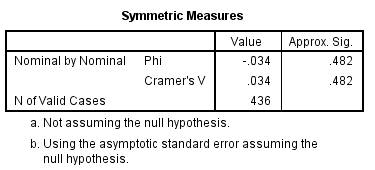
Slika-16 Symmetric Measures [Izvor: sopstvena izrada]
Pretpostavke
Najpre treba proveriti da li je prekršena jedna od pretpostavki testa hi-kvadrat u pogledu najmanje očekivane ćelijske učestalosti, koja bi trebalo da bude 5 ili više (ili da najmanje 80 procenata ćelija ima očekivane učestalosti 5 ili više). Ta informacija je data u fusnoti ispod tabele Chi-Square Tests. U fusnoti a u primeru kaže se "0 cells (,0%) have expected count less than 5. The minimum expected count is 35,87". To znači da nismo prekršili pretpostavku, pošto su očekivane učestalosti u svim ćelijama veće od 5 (u našem primeru, veće od 35,87).
Hi-kvadrat testovi
U rezultatima najviše nas zanima vrednost hi-kvadrat statistike (engl. Pearson Chi-Square), data u tabeli Chi-Square Tests. Međutim, kada se ima tabela 2 sa 2 (tj. kada svaka promenljiva ima samo dve kategorije), treba upotrebiti vrednost u drugom redu tabele (Continuity Correction). To je tzv. Jejtsova korekcija (engl. Yates' Correction for Continuity); ona kompenzuje precenjenu vrednost hi-kvadrat koja je posledica malog broja dimenzija tabele 2 sa 2. U gornjem primeru, korigovana vrednost iznosi 0,337, uz značajnost 0,56 (datu u koloni Asymp. Sig. (2-sided)). Da bi rezultat bio značajan, veličina Sig. treba da je 0,05 ili manja. U ovom primeru, vrednost 0,56 je (11 puta) veća od alfa vrednosti 0,05, pa možemo zaključiti da naš rezultat nije značajan. To znači da se proporcija muškaraca koji puše ne razlikuje od proporcije žena koje puše. Drugim rečima, nema nikakve veze između pušačkog statusa i pola. Time je potvrđena nulta hipoteza.
Unakrsno tabeliranje
Procenat pušača svakog pola može se očitati u zbirnim informacijama datim u tabeli sex * smok Crosstabulation. S toliko informacija naguranih u svaku ćeliju, ova tabela vas može zbuniti. Da biste saznali koji procenat muškaraca su pušači, pročitajte prvi red tabele koji se odnosi na muškarce. U ovom slučaju, gledamo šta piše u nastavku % within sex. U ovom primeru , 17,9% procenata muškaraca su pušači i 82,1 procenata nepušači; 20,6 procenata žena je pušača i 79,4 procenata nepušača. Kako biste bili sigurni da čitate ispravne vrednosti, proverite da li zbir te dve procentualne vrednosti iznosi 100%.
Da nas zanima procenat celog uzorka koji spada u pušače, prešli bismo naniže u poslednji red, koji sabira rezultate za oba pola. U ovom slučaju, pogledali bismo šta piše u redu % of Total. Prema tim rezultatima, 19,5 procenata uzorka puši, a 80,5 procenata ne puši.
Veličina uticaja
U proceduri Crosstabs izračunava se više pokazatelja veličine uticaja (tj. jačine veze između promenljivih). Za tabele 2 sa 2, najčešće se koristi koeficijent fi (phi coefficient), što je koeficijent korelacije u opsegu od 0 do 1, pri čemu veći broj pokazuje jaču vezu između dve promenljive. U ovom primeru, koeficijent fi (prikazan u tabeli Symmetric Measures) iznosi -0,034, što se smatra vrlo malim uticajem po Koenovom (1988) kriterijumu od 0,10 za mali, 0,30 za srednji i 0,50 za veliki uticaj.
Za tabele veće od 2 sa 2, u izveštaj treba staviti Kramerov pokazatelj V (Cramer's V), koji uzima u obzir broj stepeni slobode. Za ocenu veličine uticaja kod većih tabela koriste se malo drugačiji kriterijumi. Da biste utvrdili koji kriterijum da upotrebite, najpre oduzmite 1 od broja kategorija u rednoj promenljivoj (R-1), a zatim oduzmite 1 od broja kategorija u kolonskoj promenljivoj (K-1). Od ta dva broja, zadržite onaj manji.
Za R-1 ili K-1 jednako 1 (dve kategorije): mali = 0,01, srednji = 0,30 i veliki = 0,50.
Za bilo R-1 bilo K-1 jednako 2 (tri kategorije): mali = 0,07, srednji = 0,21 i veliki = 0,35.
Za bilo R-1 bilo K-1 jednako 3 (četiri kategorije): mali = 0,06, srednji = 0,17 i veliki = 0,29.
Rezultate ove analize mogli biste predstaviti ovako: Hi-kvadrat test nezavisnosti (uz korekciju neprekidnosti prema Jejtsu) nije pokazao značajnu vezu između pola i pušačkog statusa, X2 (1, n = 436) = 0,34, p = 0,56, fi = -0,034.
Preuzeto iz: Pallant, J. (2011), SPSS: priručnik za preživljavanje (prevod 4. izdanja), Beograd: Mikro knjiga
