- Očekivane vremenske rezerve i verovatnoće realizacije kritičnog puta
- Verovatnoće realizacije kritičnog puta
- Primer određivanja verovatnoće realizacije kritičnog puta
- Primer1 određivanja verovatnoće realizacije kritičnog puta
- Primer određivanja verovatnoće realizacije kritičnog puta -rešenje
Vremenska rezerva određenog događaja, označena sa Δei , predstavlja vremensku razliku između očekivanog najkasnijeg i najranijeg vremena nastupanja posmatranog i-tog (ili j-tog) događaja, tj:
Δei = tei1 - tei0 , i = 1, 2, ..., n
Očekivana vremenska rezerva u događaju može biti pozitivna ili jednaka nuli (negativna vrednost vremenske rezerve bi ukazivala na manjak kapaciteta pri realizaciji projekta):
- pozitivna vremenska rezerva inicira mogućnost završetka neke aktivnosti pre planiranog roka (višak kapaciteta),
- kada je jednaka nuli, kapaciteti su procenjeni kao adekvatni, ali istovremeno, i kritični. Kritični događaji imaju vremensku rezervu jednaku nuli.
U MD nekog projekta postoji više puteva od početnog do završnog događaja. Jedan ili više njih se identifikuje kao kritičan put Pc , i on predstavlja niz međusobno povezanih (rednih) aktivnosti, sumarno sa najdužim očekivanim vremenom trajanja.
Da bi neki događaj pripadao očekivanom kritičnom putu, potreban i dovoljan uslov je da je
tei1 = tei0
Dakle, aktivnost (i – j) je na kritičnom putu ako je:
tej1 - tei0 - teij = 0
Od posebnog je interesa određivanje verovatnoće ispunjavanja planiranih rokova.
Često se, kod planiranja realizacije projekta PERT metodom, za neke događaje u MD unapred utvrde termini, rokovi njihovog ispunjenja. Za ovakve događaje značajno je proceniti verovatnoću njihovog odigravanja u okviru planiranog roka.
Neka se označi sa Tp planirani rok odigravanja događaja, npr. poslednjeg događaja, a sa z odgovarajući faktor verovatnoće, koji se može izračunati kao standardizovana (centrirana) vrednost sume aktivnosti na kritičnom putu. Dakle:
Verovatnoća ostvarenja P(z) nekog događaja u MD u predviđenom roku je važan podatak značajan planerima,. a određuje se u funkciji faktora verovatnoće Z, a za izračunatu vrednost faktora Z najlakše očitavanjem sa grafika (slika 1) ili iz tablice (u tabeli 1 date su verovatnoće P u funkciji faktora verovatnoće Z).
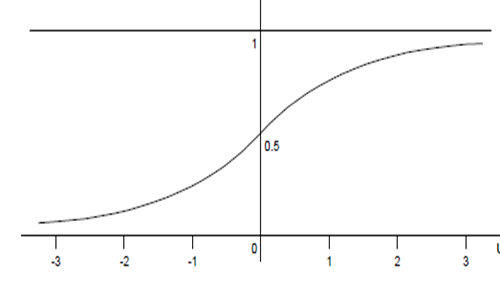
Slika-1 Dijagram raspodele funkcije P(z) za različite vrednosti faktora z (Izvor: OM320-NM-2019/20)
P(z) - verovatnoća odigravanja događaja prikazana je u tabeli 3.4. Za zadati (izračunati) faktor verovatnoće z u tabeli su date vrednosti verovatnoće P(z). Za vrednosti z >3 vredosti verovatnoće P(z) je približno jedan, dok za vrednosti z < 3 vrednosti P(z) su približno jednake nuli.
Ako je z < 0 , onda se vrednosti P(-z) mogu odrediti izrazom 1-P(z), gde je z>0 .
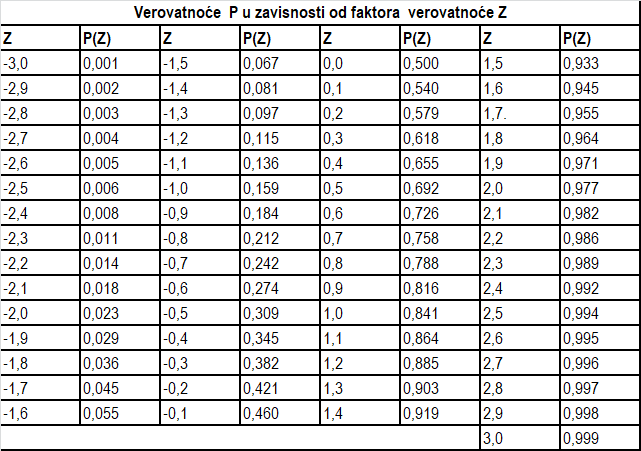
Slika-2 Tabela1 P(z) - verovatnoća odigravanja događaja (Izvor: OM320-NM-2019/20)
Gde su:
σ2 – zbir varijansi i
te – zbir očekivanih vremena aktinosti (i – j) koje prethode poslednjem događaju n, a leže npr. na kritičnom putu Pc .
Vrednosti verovatnoća P(z) se najčešće predstavljaju tabelarno, ili određuju npr. preko MS Excel funkcija.
Napomena:
Standardizovana normalna distribucija je oblik normalne distribucije, gde je vrednost aritmetičke sredine jednaka nuli, a vrednost standardne devijacije je jednaka 1. Za praktična izračunavanja koristi se tablica približnih vrednosti funkcije raspodele F(x).
Primer
Za polazne podatke date u tabeli1 izvršiti analizu vremena po metodi PERT.
projektovati mrežni dijagram,
odrediti očekivano vreme teij i varijansu σij2 za svaku aktivnost,
odrediti očekivani kritičan put Pc .
Izračunati verovatnoću nastupanja završnog događaja, ako je planirano vreme završetka kritičnih aktivnosti Tp=20.
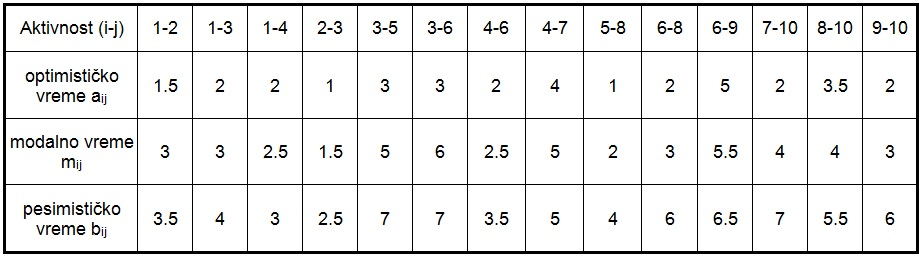
Slika-3 Tabela-2: Lista aktivnosti (Izvor: OM320-NM-2019/20)
Rešenje:
Slika 1 je prikazuje mrežni plan za primer.
Određivanje očekivanih vremena i varijansi prikazano je na slici 2.
Kritični put u mreži dobija se u rezultatu analize svih puteva na osnovu očekivanih vremena, odnosno njihovih suma, npr.

Slika-4 Kritični put (Izvor: OM320-NM-2019/20)
Određivanje očekivanih vremena i varijansi i verovatnoće prikazano je na slici 2
Na osnovu faktora verovatnoće z = 0,943, uz dodatnu interpolaciju je:
P(z)=P(0.943)=0.8268 (82.68%)
što predstavlja relativno visoku izvesnost (verovatnoću) u pogledu roka završetka kritičnih aktivnosti u odnosu na planirani rok.
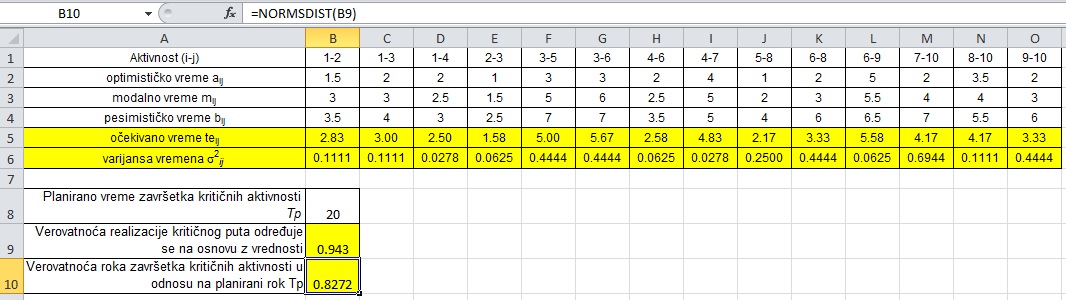
Slika-5 Primer analize vremena po metodi PERT (Izvor: OM320-NM-2019/20)
