Domaći zadatak

Domaći zadatak 3

Domaći zadatak 3
Domaći zadatak 3 - 3. i 4. zadatak
Domaći zadatak 3 - 5. i 6. zadatak
Domaći zadatak 3 - 7. i 8. zadatak

Domaći zadatak 3

Domaći zadatak 3 obuhvata sadržaj lekcija 6-9 i sastoji se od 4 zadatka. Ostale informacije se nalaze u planu i program predmeta. (procenjeno vreme: 30 min)

Zadatak 1

Problem ILP je rešen pomoću simpleks tabele, a optimalno rešenje je prikazano u tabeli 1 .

Optimalno rešenje je necelobrojno.

Odrediti izdvojeno ograničenje.

Odrediti dopunsko ograničenje.

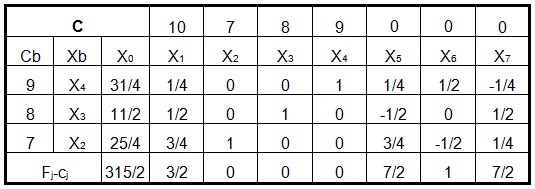
Slika-1 Tabela-1: Simpleks tabela (Izvor: OM320-NM-2019/20)

Zadatak 2

Problem je rešen pomoću simpleks tabele, a optimalno rešenje je prikazano u tabeli 2 .

Optimalno rešenje je necelobrojno.

Odrediti izdvojeno ograničenje.

Odrediti dopunsko ograničenje.

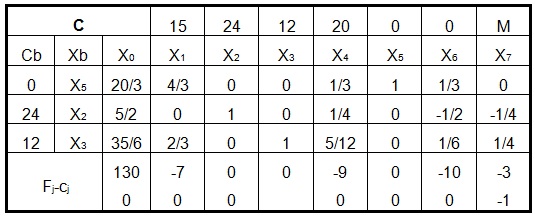
Slika-2 Tabela-2: Simpleks tabela (Izvor: OM320-NM-2019/20)

Domaći zadatak 3 - 3. i 4. zadatak

Domaći zadatak 3 - 3. i 4. zadatak (procenjeno vreme: 30 min)

Zadatak 3

Dva igrača A i B igraju šah. U trenutku prekida igrač A se nalazi u šahu. On ima na raspolaganju tri moguća poteza i treba da kovertira potez. Igrač B je, u prekidu, analizirao poziciju i pronašao da ima na raspolaganju četiri moguća poteza. Sačinio je matricu plačanja u zavisnosti od poteza koji je kovertirao igrač A i poteza koji bi trebalo da odigra igrač B, slika 1 .

Pri čemu elementi matrice plaćanja predstavljaju verovatnoće dobijanja partije za oba igrača, sa pozitivnim znakom znače da igrač A stiče bolju poziciju, a sa predznakom minus da igrač B ima bolju poziciju, nula znači remi poziciju.

Koji je potez najsigurniji za igrača A?

Koji je najbolji odgovor igrača B?

Kako izgleda pozicija posle odigrana dva poteza?

Slika-3 Matrica plaćanja (Izvor: OM320-NM-2019/20)

Zadatak 4

Crtanje mrežnog dijagrama i analiza vremena po CPM metodi.

Za projekat je dat spisak aktivnosti, njihova vremenska zavisnost i vreme trajanja u tabeli 3 . Postaviti mrežni dijagram i odrediti najkraće vreme realizacije projekta.

Karakteristično za ovaj zadatak je da se zavisnost aktivnosti E od aktivnosti A i B može pravilno prikazati samo ako se uvede poseban događaj za početni događaj aktivnosti E. U taj događaj moraju da uđu dve veštačke aktivnosti. Naime aktivnost A sama prethodi aktivnosti D, a zajedno sa B prethodi aktivnosti E.

Takođe aktivnost B zajedno sa aktivnošću C prethodi aktivnostima F i G. Pored toga u ovom primeru su se pojavile dve paralelne aktivnosti F i G.

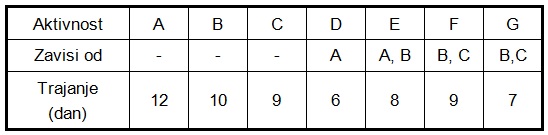
Slika-4 Tabela-3: Lista aktivnosti (Izvor: OM320-NM-2019/20)

Domaći zadatak 3 - 5. i 6. zadatak

Domaći zadatak 3 - 5. i 6. zadatak (procenjeno vreme: 30 min)

Zadatak 5

Dva igrača. Kako izgleda pozicija posle odigrana dva poteza?

Slika-5 Matrica plaćanja (Izvor: OM320-NM-2019/20)

Zadatak 6

Crtanje mrežnog dijagrama i analiza vremena po CPM metodi.

Za projekat je dat spisak aktivnosti, njihova vremenska

Slika-6 Tabela-3: Lista aktivnosti (Izvor: OM320-NM-2019/20)

Domaći zadatak 3 - 7. i 8. zadatak

Domaći zadatak 3 - 7. i 8. zadatak (procenjeno vreme: 30 min)

Zadatak 7

Konstruisati mrežni dijagram primenom CPM metode, odrediti vremenske rezerve i kritičan put ako su poznate međusobne zavisnosti između aktivnosti:
A,B,J →
C,D → A
E → B
F → B,D
G → C
H → C,D,F
I → E,J
K → I,G,H
kao i njihova vremena trajanja:

Slika-7 Vremena trajanja aktivnosti (Izvor: OM320-NM-2019/20)

Zadatak 8.

Konstruisati MD za projekta korišćenjem metode PERT i odrediti:
a) najranija i najkasnija vremena ostvarenja događaja i njima pripadajuće varijanse, očekivane vremenske rezerve i verovatnoću da će se očekivane vremenske rezerve dogoditi
b) verovatnoću realizacije projekta u unapred planiranom terminu od 26 vremenskih jedinica.
Poznati su podaci o vremenu trajanja aktivnosti i njihovim zavisnostima:

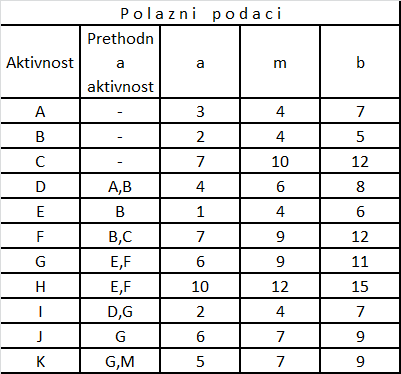
Slika-8 Vremena trajanja i međuzavisnost aktivnosti (Izvor: OM320-NM-2019/20)