- Određivanje vremenskih rezervi po CPM metodi
- Zadatak 1 analiza vremena po CPM metodi
- Zadatak 1 analiza vremena po CPM metodi - rešenje
- Određivanje vremena realizacije projekta i kritičnog puta - video
Aktivnosti kod kojih je maksimalno dozvoljeno vreme trajanja (tj1 - ti0 ) veće od njihovog trajanja tij imaju određenu vremensku rezervu za njihovo izvršenje. To su tzv. nekritične aktivnosti. Podatak o vremenskoj rezervi pokazuje za koliko vremenskih jedinica može biti odložen početak pojedinih aktivnosti, a da to ne utiče na konačni rok završetka celog projekta. Kod analize vremena po CPM metodi postoji nekoliko vrsta vremenskih rezervi, a to su:
Ukupne vremenske rezerve Δuij aktivnost (i – j), slika 1.
Δuij=tj1 - ti0 - tij
Slobodne vremenske rezerve Δsij aktivnost (i – j)
Δsij =tj0 - ti0 - tij
Ukupna vremenska rezerva pokazuje za koliko možemo pomeriti vreme najranijeg početka aktivnosti, a da pri tome – krajnji rok završetka projekta ne bude pomeren. Slobodna vremenska rezerva pokazuje za koliko možemo produžiti trajanje aktivnosti ili pomeriti njen najraniji početak, pa da sve naredne aktivnosti zadrže najranije vreme početka.
Ovu vremensku rezervu mogu imati samo aktivnosti kod kojih završni događaj zavisi od završetka više aktivnosti. Nezavisna vremenska rezerva pokazuje za koliko se može pomeriti izvršenje neke aktivnosti i pored toga što je događaj dostignut u najkasnijem dozvoljenom vremenu, pa da to ne utiče na najraniji početak narednih aktivnosti. Ona se izračunava preko sledećeg izraza:
Δnij =tj0 - ti1 - tij
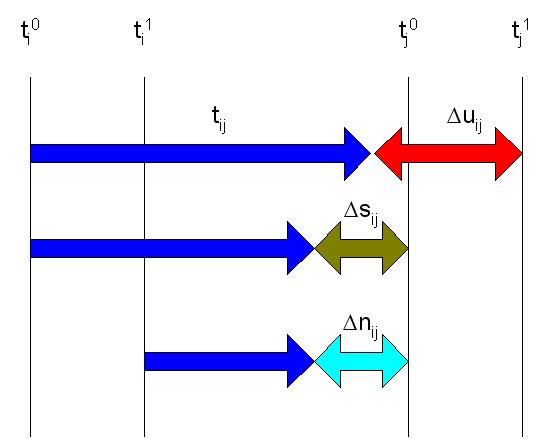
Slika-1 Određivanje vremenskih rezervi (Izvor: OM320-NM-2019/20)
Zadatak 1
Za projekat je dat spisak aktivnosti, njihova vremenska zavisnost i vreme trajanja u tabeli 1.
Postaviti mrežni dijagram i odrediti najkraće vreme realizacije projekta.
Karakteristično za ovaj zadatak je da se zavisnost aktivnosti E od aktivnosti A i B može pravilno prikazati samo ako se uvede poseban događaj za početni događaj aktivnosti E. U taj događaj moraju da uđu dve veštačke aktivnosti. Naime aktivnost A sama prethodi aktivnosti D, a zajedno sa B prethodi aktivnosti E.
Na mrežnom dijagramu, slika 2, koji odgovara zadatku, postoji graška. Navedite je.
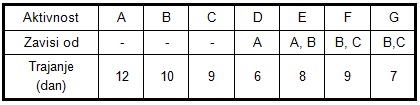
Slika-2 Tabela-1: Lista aktivnosti (Izvor: OM320-NM-2019/20)
Rešenje
U ovom zadatku se pojavljuju dve paralalne aktivnosti F i G. Kako se ne može dozvoliti da im budu isti početni i završni događaj uvedena je veštačka aktivnost, što na slici 1 nije prikazano isprekidanom linijom.
Najkraće vreme za koje se može realizovati projekat je 20 dana, slika 3.
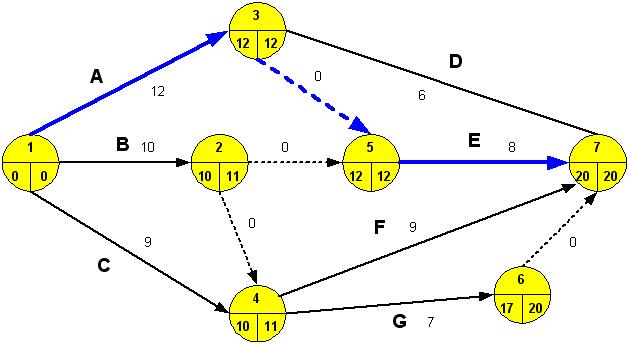
Slika-3 Najkraći put - rešenje zadatka 1 (Izvor: OM320-NM-2019/20)
Pogledajte video Critical Path Method (CPM).
Pogledajte video kako se određuje kritičan put i rok realizacije projekta
