Vežba - Crtanje mrežnog dijagrama i analiza vremena po CPM metodi

Vežba

Vežba - izrada dijagrama po CPM metodi
Vežba - analiza vremena po CPM metodi
Vežba - analiza vremena po CPM metodi - komentari
Vežba 2- analiza vremena po CPM metodi
Vežba - analiza vremena po CPM metodi - video

03

Vežba - izrada dijagrama po CPM metodi

Opis zadatka i rešenje

Opis zadatka

Za projekat je dat spisak aktivnosti, njihova vremenska zavisnost i vreme trajanja u tabeli 1 .

Postaviti mrežni dijagram i odrediti najkraće vreme realizacije projekta.

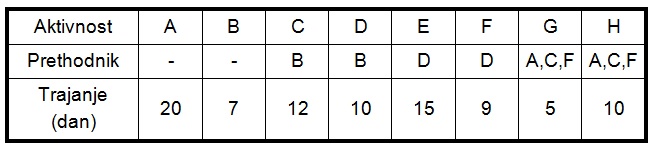
Slika-1 Tabela-1: Lista aktivnosti (Izvor: OM320-NM-2019/20)

Rešenje zadatka

Vremanska zavisnost aktivnosti može da se prikaže pomoću kvadratne tabele međusobnih odnosa, tabela 2 .

Slika-2 Tabela-2: Tabela međusobnih odnosa (Izvor: OM320-NM-2019/20)

Na osnovu tabele međusobnih odnosa i pravila za crtanje MD postavljen je MD i izvršeno numerisanje događaja po pravilu Fulkersona, slika 1 .

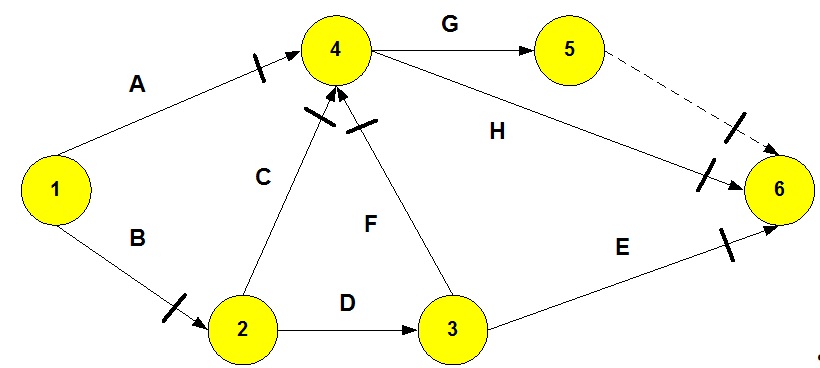
Slika-3 Mrežni dijagram projekta (Izvor: OM320-NM-2019/20)

Vežba - analiza vremena po CPM metodi

Određivanje kritičnog puta

Analiza vremena je izvršena na mrežnom dijagramu na slici2.

Analiza počinje izračunavanjem vremena najranijeg završetka pojedinih aktivnosti prema izrazu:

${t_{j}}^{0} = \underset{i}{m a x} ({t_{i}}^{0} + t_{i j})$ pri čemu je

t₁⁰=0, i < j, j = 2, 3, ..., n.

Vremena su upisana u levim delovima krugova (događaja) MD.

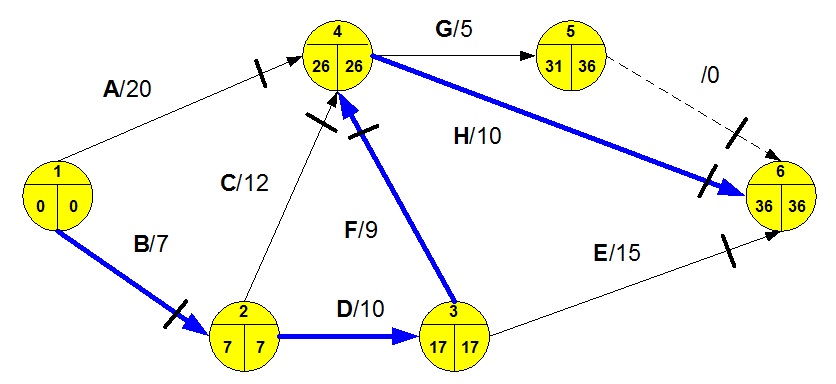
Slika-4 Analiza vremena MD (Izvor: https://pdfcoffee.com/operaciona-istrazivanja-knjiga-dopuna-2-mrezno-planiranje-pdf-free.html)

Pošto se odredi vreme najranijeg završetka projekta t_n⁰ , usvaja se t_n¹=t_n⁰ .

Sada se određuju vremena najkasnijih početaka aktivnosti:

${t_{i}}^{1} = \underset{j}{m i n} ({t_{j}}^{1} - t_{i j})$ , pri čemu je

i = n-1, n-2, ..., 1

Ova vremena su upisana u desne delove krugova (događaja), slika2.

Treći korak je određivanje kritičnog puta.

Kritični put ide preko kritičnih događaja, tj. događaja kod kojih je

t_i⁰= t_i¹ i t_j⁰= t_j¹

Kritične aktivnosti moraju da ispune još jedan uslov:

njihova ukupna vremenska rezerva je jednaka 0, tj.

t_j¹ - t_i⁰= t_ij

Kritični put je (1-2)(2-3)(3-4)(4-6), a zbir vremena je: 7 + 10 + 9 + 10 = 36

Vežba - analiza vremena po CPM metodi - komentari

Komentari u vezi analize vremena po CPM metodi

Komentar

Najraniji početak aktivnosti (i – j) označava se najranijim događajem t_j⁰ po metodologiji CPM.

Najraniji završetak celog projekta nastupa posle isteka vremena t_n⁰

t_i⁰ – najraniji (mogući) početak aktivnosti A_ij

t_i¹ - najkasniji (dozvoljeni) početak aktivnosti A_ij

t_j⁰ – najraniji (mogući) završetak aktivnosti A_ij

t_j¹ – najkasniji (dozvoljeni) završetak aktivnosti A_ij

Najraniji završetak (tzv. rano vreme) proizvoljne aktivnosti (i – j), koji se označava sa t_j⁰ , dobija se kao:

t_j⁰ = t_i⁰ + t_ij

Ako je neki događaj A_j završni događaj za više aktivnosti, pri čemu sve te aktivnosti nemaju isto trajanje, onda taj događaj može nastupiti tek posle završetka aktivnosti sa najdužim vremenom trajanja, tj: ${t_{j}}^{0} = \underset{i}{m a x} ({t_{i}}^{0} + t_{i j})$ , pri čemu je

t₁⁰ = 0, i < j, j = 2, 3, ..., n

Ako je poznat planirani rok završetka celog projekta T_p on će biti ostvaren jedino ako je

t_n⁰ ≤ T_p

Ukoliko se desi da je t_n⁰ > T_p, projekat ne može biti završen u planiranom roku, pa je potrebno izvršiti skraćivanje trajanja nekih aktivnosti dok se ne dostigne planirani rok.

${t_{i}}^{1} = \underset{j}{m i n} ({t_{j}}^{1} - t_{i j})$ , pri čemu je

t_n¹ =t_n⁰=T_p , i < j, i = n-1, n-2, ..., 1, t₁¹ = t₁⁰ = 0

Vežba 2- analiza vremena po CPM metodi

Primer 2 analize vremena po CPM metodi

Opis zadatka

Konstruisati mrežni dijagram korišćenjem metode CPM, odrediti kritičan put i vremenske rezerve ako su poznata vremena trajanja aktivnosti, kao i njihove međuzavisnosti:

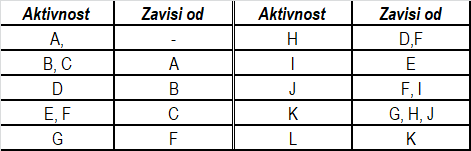
Slika-5 Tabela1 Međuzavisnosti aktivnosti (Izvor: OM320-NM-2019/20)

Za razmatrani primer odrteđena su vremena trajanja svake aktivnosti pojedinačno i data u tabeli 2

Proračun najranijh vremena početaka aktivnosti (proračun vremena događaja) vrši se progresivnim računanjem vremena idući od početnog i sabirajuči sukcesivno vremena do završnog događaja (slika 7).

Kritičan put obuhvata kritične aktivnosti A, C, F, G, K i L u ukupnom trajanju: (3 +4 +4 + 9 + 1 + 7 ) = 28 v.j. To određeno je ukupno vreme trajanja projekta.

Vežba - analiza vremena po CPM metodi - video

Activity Networks and Critical Path Analysis

Pogledajte Activity Networks and Critical Path Analysis.