- Definicija i grafik funkcije dve promenljive
- Primer
- Autorski video klip
- Video klip
- Dvodimenzionalna oblast
$\textbf{Definicija. }$ $\color{red} {\text{Realna funkcija dve realne promenljive}}\,\,\,$ je bilo koje pravilo ili zakon po kome se svakom uređenom paru $ ( x , y ) $ iz nekog skupa $ A ⊆ \mathbb{ R } ^ 2 $ pridružuje tačno jedan broj $ z ∈ B ⊆ \mathbb{ R } . $
Napomena. Ubuduće ćemo realnu funkciju dve realne promenljive kraće zvati funkcija dve promenljive.
Funkciju dve promenljive u eksplicitnom obliku zapisujemo sa $ z = f ( x, y ) . $ Ona može biti data u parametarskom, kao i u implicitnom obliku (analogno slučaju kod funkcije jedne promenljive).
Oblast definisanosti funkcije dve promenljive je skup tačaka $(x,y) \in \mathbb R^2$ za koje $ z= f ( x , y ) $ može da se odredi. Ovde važe iste napomene u vezi sa oblašću definisanosti kao i kod funkcije jedne promenljive.
Grafik generisan realnom funkcijom dve realne promenljive (videti sliku) predstavlja skup tačaka u $ ℝ ^ 3 $ dat sa $$ Г_f = \{ \big( x , y , f ( x , y ) \big) \mid ( x , y ) ∈ D \} ⊆ \mathbb{ R } ^ 3. $$
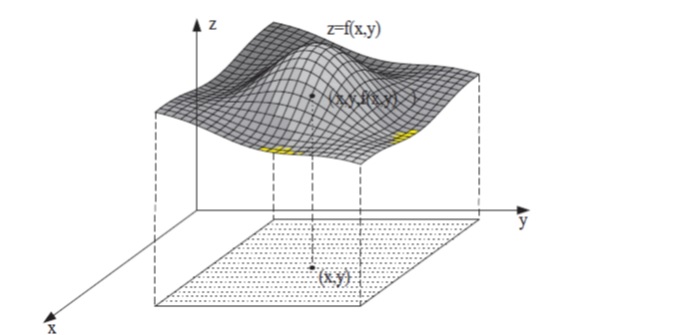
Slika-1.1: Grafik realne funkcije dve realne promenljive [Izvor: Autor].
U našem razmatranju isključivo ćemo se baviti funkcijama koje će za grafik imati neprekidnu, ili na malom delu prekidnu površ.
Napomena. Na način kako je definisana funkcije dve promenljive, analogno se može definisati i funkciju tri ili više promenljivih.
a) U ovom slučaju nema nikakvih ograničenja, pa je domen $\mathbb{ R }^2.$
b) Zbog korena parnog reda neophodno je da bude $ 1 - x ^ 2 \geq 0 $ i $ y ^ 2 - 1 \geq 0 . $ Tada je domen ove funkcije skup $$ \big\{ ( x , y ) \in \mathbb{ R }^2 \mid x \in[ - 1 , 1 ] \wedge y \in( - \infty , - 1 ] \cup [ 1 , + \infty ) \big\}. $$
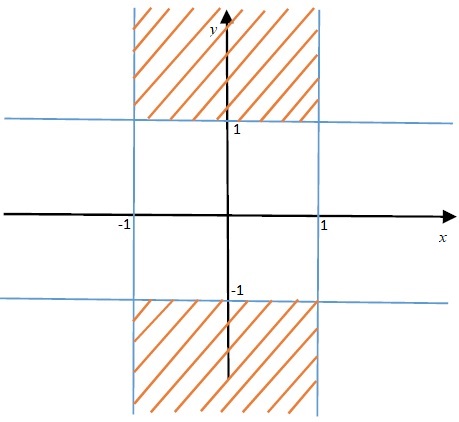
Slika-1.2: Domen funkcije $z=\sqrt{1-x^2}+\sqrt{y^2-1}$ [Izvor: Autor].
c) Zbog logaritamske funkcije mora biti $ 4 - x ^ 2 - y ^ 2 > 0 , $ tj. $ x ^ 2 + y ^ 2 < 4 . $ Dakle, domen ove funkcije je unutrašnjost kruga $ x ^ 2 + y ^ 2 = 4 , $ bez kružnice, tj. $$ \big\{ ( x , y ) \in\mathbb{ R } ^ 2 \mid x ^ 2 + y ^ 2 < 4 \big\}. $$
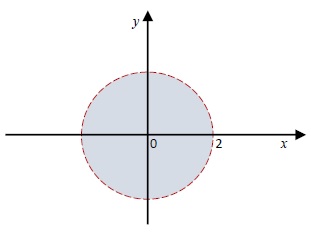
Slika-1.3: Domen funkcije $z=\ln(4-x^2-y^2)$ [Izvor: Autor].
d) Kako imamo koren neparnog reda, zbog njega nema nikakvih ograničenja i jedino ograničenje je $ x ^ 2 + y ^ 2 \neq 0 , $ tj. $$ \big\{ ( x , y ) \in\mathbb{ R } ^ 2 \mid x \neq 0 \wedge y \neq 0 \big\}. $$ Dakle, domen funkcije su sve tačke iz ravni, bez koordinatnog početka, tj. $\mathbb R^2\setminus\{(0,0)\}$.
$\bf Definicija.\,\,$ U prostoru $ ℝ ^2 $ za skup se kaže da je $\color{red} {\text{otvoren}}$ ako i samo ako se oko svake njegove tačke može opisati krug koji ceo pripada njemu.
$\bf Definicija.\,\,$ U prostoru $ ℝ ^2 $ za skup se kaže da je $\color{red} {\text{povezan}}$ ako i samo ako je putno povezan.
Napomena. Neki skup je putno povezan ako svake dve njegove različite tačke možemo spojiti putem koji ceo pripada skupu (put je bilo koja neprekidna kriva u $ ℝ ^2 $).
$\bf Definicija.\,\,$ Neki skup nazivamo $ \color{red} {\text{oblast u } ℝ ^ 2} $ ili $\color{red} {\text{dvodimenzionalna oblast}}\,\,\,$ ako i samo je taj skup otvoren i povezan u prostoru $ ℝ ^2 ,$
$\bf Definicija.\,\,$ Tačka $ A $ se naziva $\color{red} {\text{granična tačka neke oblasti}}\,\,\,$ $ E $ ako i samo ako svaka okolina tačke $ A , $ pored tačaka iz oblasti $E , $ sadrži i tačke koje ne pripadaju oblasti $ E . $
Skup svih graničnih tačaka neke oblasti $ E $ nazivamo $\color{red} {\text{granica oblasti}}\,\,$ i označavamo $ ∂ E . $
Ako nekoj otvorenoj oblasti $ E $ pridružimo sve njene granične tačke dobijamo skup tačaka koje zovemo $\color{red} {\text{zatvorena oblast}}\,\,$ i nju označavamo sa $ \overline{ E } $ (tj. važi $ \overline{ E } = E ∪ ∂ E $).
Ako za datu oblast možemo naći krug konačnog poluprečnika, koji pokriva tu oblast, onda tu oblast nazivamo $\color{red} {\text{ograničena oblast}}.\,\,$ U suprotnom oblast nazivamo $\color{red} {\text{neograničena oblast}}.\,\,$
